1 引言

中国作为一个拥有庞大人口的国家，在处理相关问题时必须更加专业和深入。人口出生率是我们关注的核心指标，它不仅反映了增长速度，也是制定综合性决策的重要依据。自计划生育政策实施以来，我国的出生率逐渐稳定在较低水平。然而，随着时间的推移，我们开始认识到当前低出生率可能带来的潜在风险，如老龄化和劳动力不足。因此，在未来的政策制定中，必须全面考虑并深入研究相关数据与趋势。

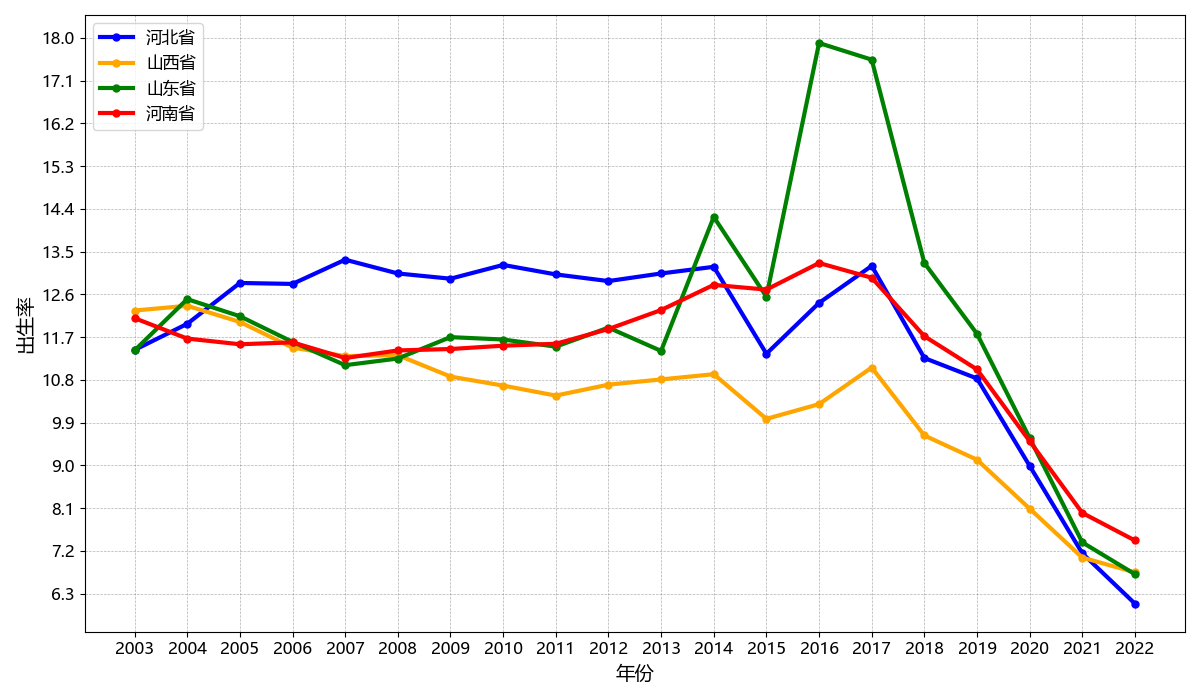
图1-1 山河四省近20年人口出生率趋势

山东、山西、河北和河南作为我国人口大省，其出生率在近年来面临严峻挑战。例如，山东省的出生率在2017年到2021年间持续下降，尤其是2020年跌破了10%。为了深入探究这四省人口出生率急剧下降的原因，本文从社会、经济和生活三个方向精选人均地区生产总值、财政支出和城镇居民人均可支配收入等多项指标进行研究。通过实验分析，我们能够更加全面准确地认知各项指标与人口出生率之间的正负相关关系及其对出生率的影响程度。

我们研究的对象是2003年至2022年间山河四省的人口出生率，选取了九个可能影响因素进行建模分析，目的是探讨哪些因素对该变量的影响最大以及其趋势预测。在对各潜在影响因素进行定性分析后，我们又介绍了所采用的建模方法及常见的评价指标。本文将描述数据并进行预处理，随后应用BP神经网络、随机森林、GBDT和XGBoost四种模型比较其拟合效果，以识别在各个模型下对该变量影响最大的因素。

2  基于机器学习的集成方法介绍

2.1   BP神经网络

BP神经网络（Back Propagation Neural Network）是一种广泛应用的前馈神经网络，具有多层结构。其核心思想是通过反向传播算法来优化网络的权重，从而有效地进行分类或回归预测。BP神经网络由输入层、隐藏层和输出层组成。每层的神经元通过权重连接，形成一个复杂的网络结构。

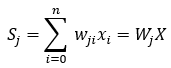
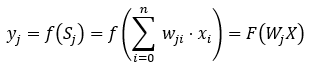
在BP神经网络中，每个神经元接收来自前一层的输入信号，并通过激活函数处理后将结果传递给下一层。通过反向传播算法，网络计算输出层的误差，并将误差逐层反向传播，更新各层神经元的权重和偏置。该过程通过梯度下降法进行优化，旨在最小化损失函数，提升模型的预测性能。具体而言，BP神经网络通过设置固定数量的隐藏层和神经元，随机初始化权重，并使用训练样本进行多轮迭代。在每一次迭代中，网络根据当前的权重和输入样本计算预测值，随后计算误差并进行反向传播，以更新权重。激活函数的选取可以为以下的非线性函数：

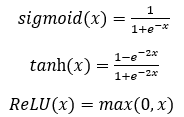
在训练完成后，BP神经网络能够对新的输入样本进行预测。BP神经网络的优势在于其灵活性和适应性，能够学习到复杂的非线性映射关系。同时，通过适当的正则化技术，可以有效地降低过拟合风险，提高模型的泛化能力。

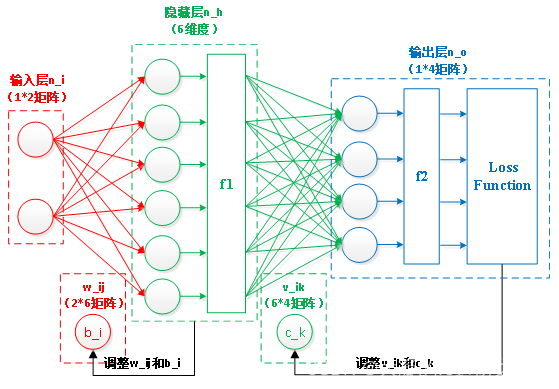
图 2-1 BP神经网络架构

2.2   随机森林

随机森林(Random Forest)，其集合了大量不相关的决策树，通过对它们的预测及过进行平均或加权平均来得到最终预测值。每次数据集都是随机有放回地选出，并且同时进行随机选择。经过特征随机抽样作为输入的处理，该算法被称为随机森林算法。随机森林算法基于Bagging方法，其估计器采用决策树模型。

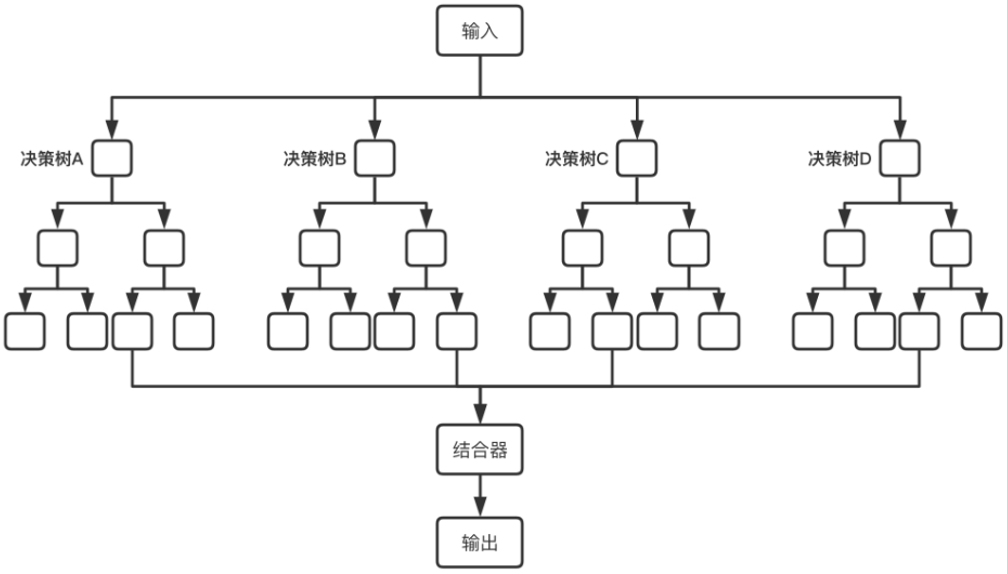
图 2-2 随机森林模型示意图

随机森林通过引入随机性来解决决策树泛化能力弱的问题，其名称中所包含的“随机”和“森林”两个关键词均具有重要意义。随机森林是一种集成学习方法，其基本思想是通过随机选择样本和特征来构建多个决策树模型，并将它们组合起来进行分类或回归预测。具体而言，每棵决策树都从整个训练样本集中选取固定数量的样本子集和特征子集进行构建，在这些独立的决策树中，对于一个输入样本，会得到N个分类结果。通过对所有分类结果进行投票并确定投票次数最多的类别作为最终输出结果，可有效减少过度拟合风险，并提升模型泛化性能。

2.3   GBDT算法

梯度提升树(GBDT)，Gradient Boosting Decision Tree，是一种Boosting算法.GBDT 算法中，每一棵决策树所学习到的内容均为前面所有决策树结论产生的误差值。这里所谓误差值即为模型对样本进行预测后得出结果与真实标签之间存在的偏离程度)，在迭代的过程中，首先需要学习回归树模型，并将真实值与预测值之间的差值作为残差。接着，以残差为目标继续学习下一棵回归树模型，并依次迭代直至达到某个预设阈值或者残差足够小，这种基于残差不断优化的方法被称为提升树算法。该方法的核心理念在于利用迭代方式，通过逐步优化模型拟合残差的过程来最小化损失函数。经过综合考虑，首棵树表现正常，而随后的所有决策均由残差所主导。最终采用梯度下降算法以减小损失函数，以达到使其取得最小值的目标(前提为损失函数可导)。输入训练数据集，损失函数GBDT算法步骤如下：

（1）对弱学习器进行初始化：

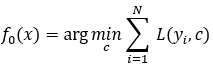
（2）对有：

（a）对每个样本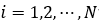计算负梯度, 即残差

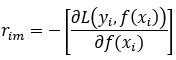
（b）利用前一步所得误差作为后续样本训练集基准值，以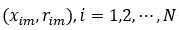作为下一个决策树模型训练数据,生成新的回归树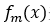并确定其对应叶子结点区域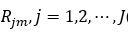(其中J表示该回归树t中叶子结点数量)。

（c）计算每个叶子区域的最优拟合值:

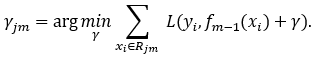
（d）更新强学习器

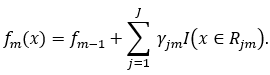
（3）得到最终学习器

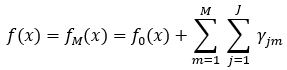
2.4   XGBoost算法

XGBoost(eXtreme Gradient Boosting)，也叫极度梯度提升树，其学习目标在于通过减少偏差来降低模型误差。为此，该方法采用多个基学习器，并确保每个基学习器都相对简单以避免过拟合。接下来的学习器将利用前面基学习器的结果和实际值之间的差值进行训练，在多次迭代中不断优化模型预测与真实值之间的误差。该算法主要采用连续生成决策树并以前一次迭代结果与目标变量之间残差作为训练数据，以减少模型偏差。通过目标函数来决定如何选择或生成一个更优的树，是在进行每一步操作时必须考虑的重要因素。目标函数包含两个主要组成部分：首先是指代样本真实值与预测值之间偏离程度的“模型误差”其次为“模型结构误差”，也称作正则化项。该项旨在通过对模型复杂性进行限制来提高其泛化能力。第t个决策树的目标函数可以表示为：

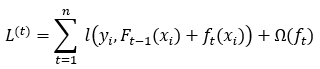
其中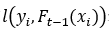表示与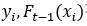有关的损失函数, 这个损失函数可以根据自己需要来定义。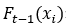表示前t?1棵决策树对样本i的预测值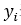；表示样本i的实际值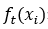；表示第t棵决策树对样本i的预测值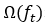；表示第t棵树的模型复杂度。

3  评价指标

（1）    MSE（均方误差）：

用于评估预测结果与实际观察结果一致性的指标，计算公式为：

（2）    MAE（平均绝对误差）：

是用来衡量预测值与实际观测值之间偏离程度的一种指标，其计算公式为：

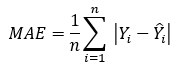
（3）    MAPE（平均绝对百分比误差）：

此指标对相对误差敏感，不会因目标变量的全局缩放改变，计算公式为：

（4）    R方（决定系数）：

表示趋势线拟合程度的指标，计算公式为：

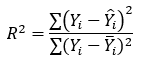
4  数据探索与预处理

数据来源于EPS数据数据库中国区域研究数据支撑平台，每一变量选取的样本为2003-2022年各年份的年度数据。为更好的将原始数据应用于实验中, 我们调用了python中的pandas，seaborn，matplotlib，sklean，numpy等函数, 建模过程中则使用了sklearn，XGBoost，GBDT，LightGBM等函数库。

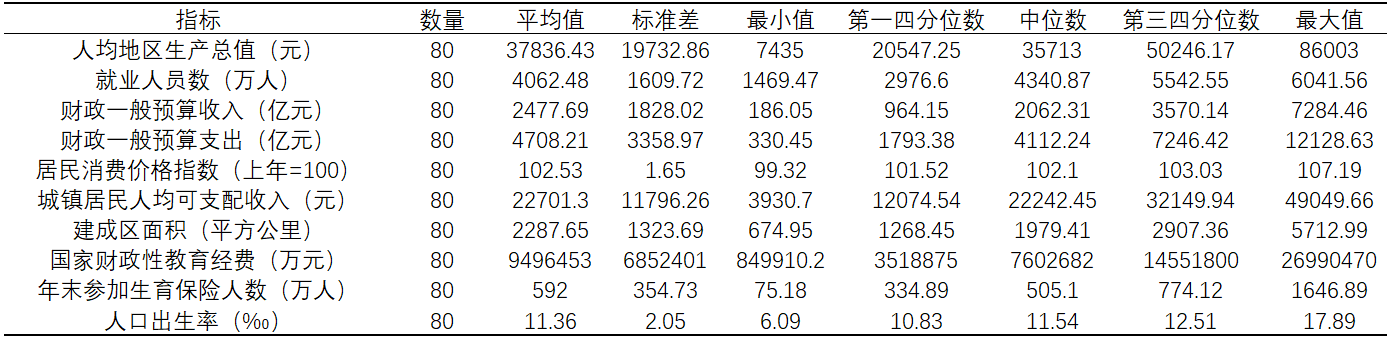
在数据处理之前做探索性分析可以更全面的了解数据，探索性分析的目的有:快速描述一份数据集；可视化数据的分布；可以更直观的了解变量的相关性关系为后续分析做基础：对给定数据，应该査看其基本情况，使用describe方法。分析集中趋势，包括均值，中位数，众数等指标。通过查看数据丢失情况，异常数据，无效的数据类型和错误值情况的分析。对原始数据进行缺失值填充（线性插值）以及异常值处理（异常值使用均值填充），对原始数据进行数值型特征描述，如下表所示：

表 4-1 山河四省人口出生率数值型描述

5 基于多模型进行预测

5.1   趋势及预测

我们可视化数据集中各个特征变量与目标变量“人口出生率（‰）”之间的关系，从而深入理解数据的特征和潜在的模式。通过回归图，观察每个特征变量与目标变量之间的线性关系，帮助识别可能的相关性和趋势。通过分布图，了解每个特征的分布情况，包括其集中趋势、偏态和可能的异常值，有助于数据处理和建模。例如：就业人数与人口生育率呈线性趋势，随着就业人数的增加，人口出生率也缓慢增加，从感性的角度分析是非常合理的，生活稳定了才有能力生儿育女。但社会的影响因素错综复杂，接下来我们将深入挖掘影响人口出生率的条件。

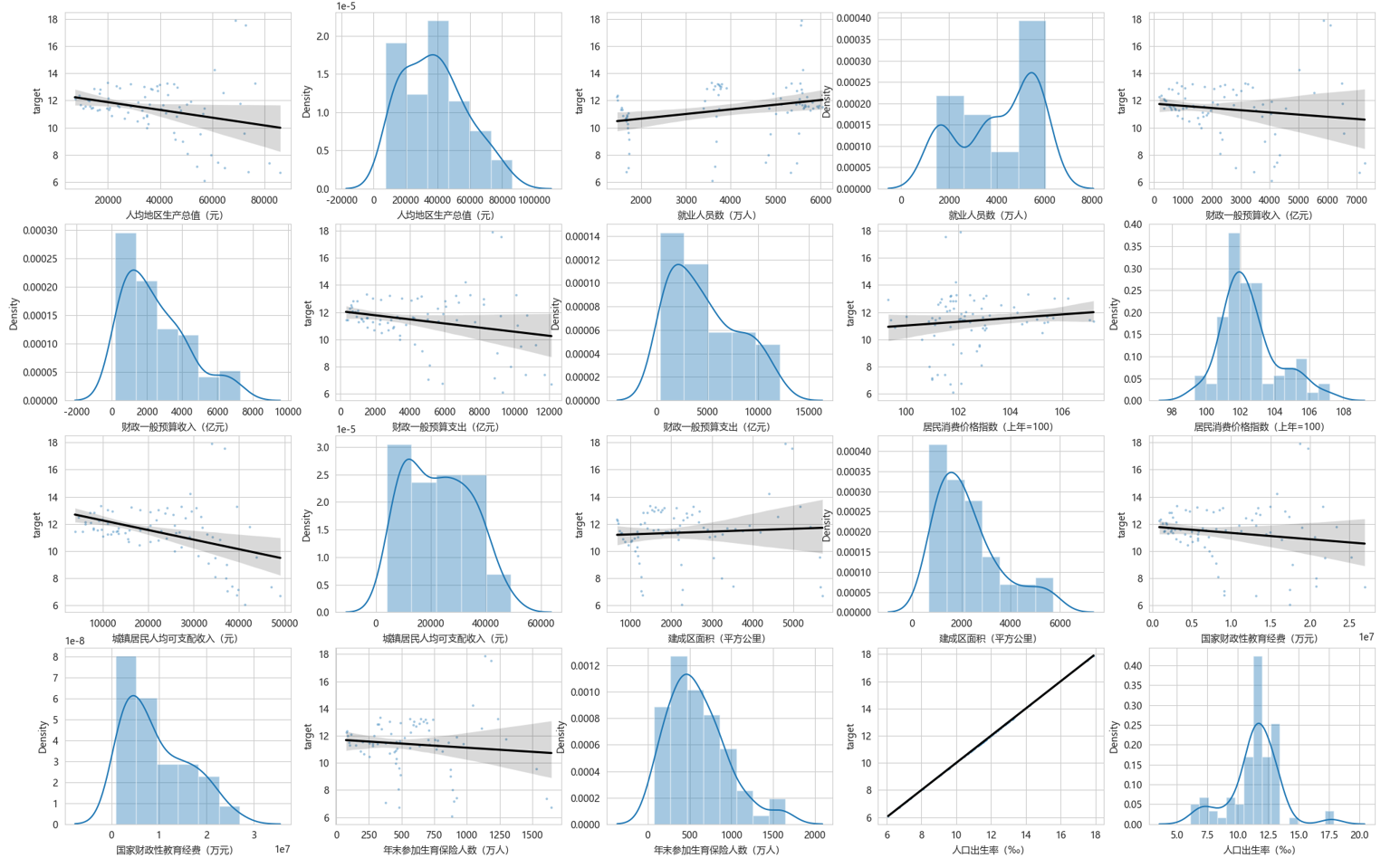
图 5-1 特征变量和人口出生率的关系

我们要将训练集与测试集中对应的特征与标签分别分离开来。我们的研究是山河四省人口出生率，因此把出生率作为标签。按8比2划分训练集与测试集，即使用python中的train_test_split方法分配训练集和测试集。分别使用BP神经网络，随机森林，GBDT以及XGBoost这四种模型来建模分析用来预测山河四省人口出生率趋势。这里评价指标采用MSE（均方误差）， MAE（平方绝对误差），RMSE（均方根误差），MAPE（平均绝对百分比误差）和R方（决定系数）。

表5-1 各类机器学习模型评分

从上述实验结果可以看出，BP神经网络模型的拟合效果较差, 随机森林模型和GBDT模型拟合效果较好，XGBoost模型的拟合效果最优。使用python中的matplotlib库绘制真实值与预测值的对比图如下：

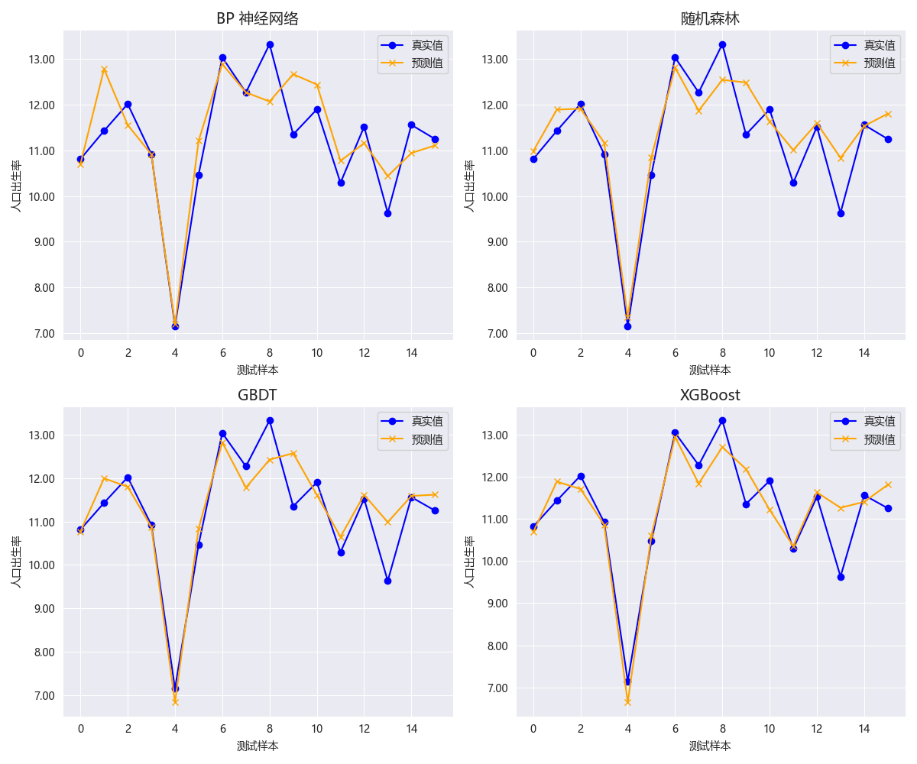
图 5-2 测试集的拟合效果图

5.2   特征重要性分析

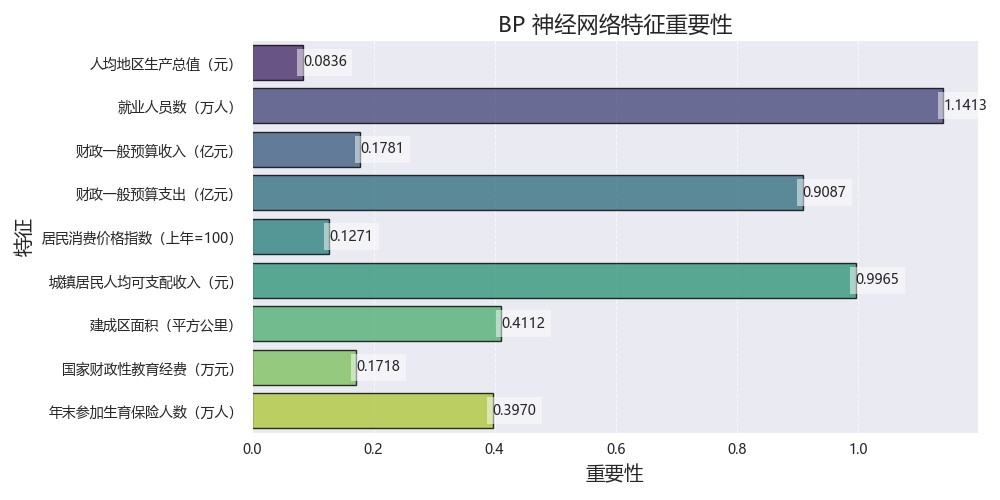
图 5-3 BP神经网络模型特征重要性排序

我们定性分析了各个变量对山河四省人口出生率的影响程度, 这里我们用python中sklearn库里面的feature-importances参数来进行特征筛选。在用BP神经网络模型进行实验时，运行结果如图所示，从图可以看出：只需要筛选出就业人数, 财政一般预算支出，城镇居民人均可支配收入这三个特征，其中就业人数的影响因素最大，考虑这三个特征为影响山河四省人口出生率的最重要变量，剩下的财政收入等特征则可以剔除。

采用BP神经网络模型，随机森林模型，GBDT模型，XGBoost模型这四种模型对样本数据进行实验，结果表明：BP神经网络模型的拟合效果不佳，原因可能是数据样本较少所致；XGBoost模型的拟合效果非常优秀，在测试集上的MSE为0.2836，并且拟合系数R²已经达到0.8761。因此在此案例中着重优化XGBoost模型，使拟合效果更优。为了使模型拟合效果更好，我们需要从现有的9个特征中选出部分特征，这样不仅降低特征维度减少计算量，也提高了模型的精度。使用python循环遍历所有可能的特征组合，筛选出的五个变量分别为人均地区生产总值，就业人数，城镇居民人均可支配收入，财政支出，居民消费价格指数。

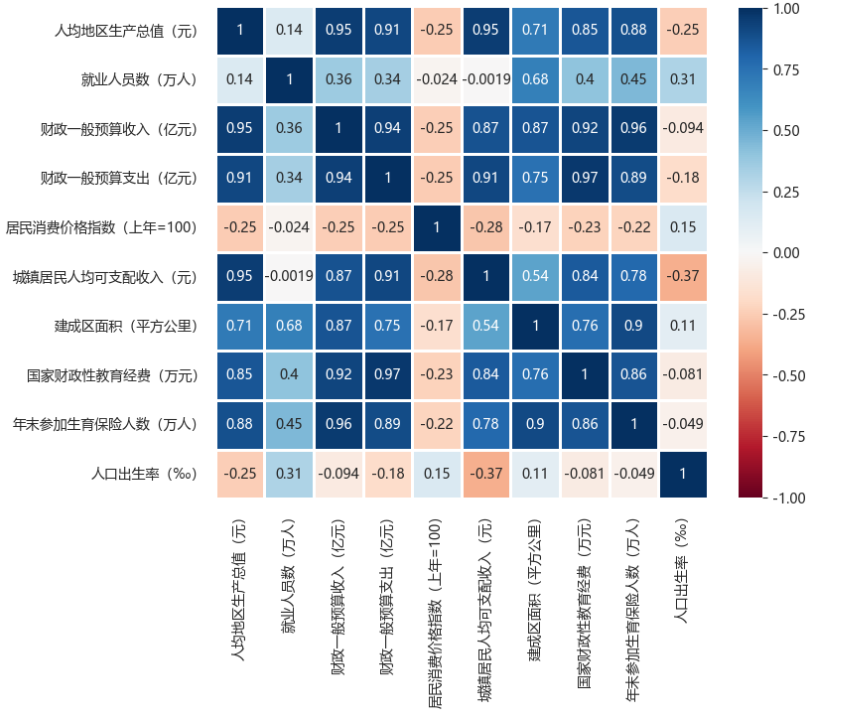
图 5-4 特征相关性热力图分析

五个特征筛选出来后再用XGBoost模型进行一次实验，它的MSE值为0.2711，RMSE值为0.5206，MAE值为0.4151，MAPE为0.0338，R²值为0.8816。与筛选特征前的实验结果对比，拟合效果有明显提升。

5.2   模型解释

采用机器学习中常见的shap值来解释模型，这是一种模型事后解释方法。其核心思想在于计算特征对模型输出的边际贡献，并从全局和局部两个层面对“黑盒模型”进行解释。shap构建了一个加性线性模型，将所有特征视为“贡献者”。为每个预测样本生成一个预测值后，模型将产生相应的shap value来表示该样本中各个特征所分配到的数值。尽管根据不同的重要性指标进行排序可能导致略微差异，但此类排名可帮助我们初步了解在模型中扮演关键角色的变量维度。需要注意的是，在实践过程中，虽然特征重要性可以揭示出哪些因素具有更高影响力，但并未涉及它们对结果产生正面或负面效果等方面信息。相较于特征重要性，Shap值在补充其不足方面具有优势.它不仅提供了变量的重要程度，还展示了影响的正负性。在全局数据集上进行不同特征Shap值的分布呈现，以下图形显示各个影响因素Shap 值的分布情况。每行表示一种特性，并以Shap值作为横轴。每个点代表一个样本，在该点处红色表示该属性具有较高数值；而蓝色则表示其具有较低数值。从图中可以看出，城镇居民人均可支配收入分布较为散乱距离0较远，说明对人口出生率的影响是最大的；其次是就业人员数，分布也较为散乱，影响排第二；其他特征的值均徘徊在0附近，说明该特征影响较小。

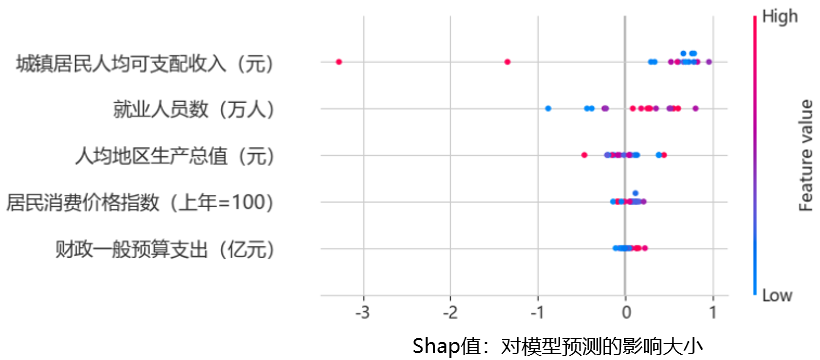
图 5-5 不同特征变量的shap值分布

为了评估变量的重要性，需要像评估特征重要性一样，在整个数据集上进行 分析。通过计算每个特征在全局数据集中的Shap值，并求出其平均数以表示 其相对贡献度大小。因此，当一个变量具有更高的平均Shapley值时，它就被认为是更加关键和显著的。因此从下图中可以看出年份，人均地区生产总值，就业人数，城镇居民人均可支配收入，财政支出以及居民消费价格指数这五个变量是较为关键的。

图 5-6 筛选后的特征重要度排序

6 总结

我们研究以山河四省人口出生率为研究对象，从EPS数据平台上选取了可能与人口出生率相关的九个变量。在定性分析的基础上利用机器学习算法做实证分析。本文使用了BP神经网络模型，随机森林模型，GBDT模型以及XGBoost模型，实验结果表明XGBoost模型是最优模型，为了优化算法从现有的9个特征中选出部分特征，这样不仅降低特征维度减少计算量，也提高了模型的精度。

针对筛选后的特征重要度的分析，城镇居民人均可支配收入对人口出生率的影响程度很大，通常与经济发展、生活水平和教育程度等因素密切相关，更高的可支配收入通常意味着更好的生活条件，这可能是人们在生育方面最直接的影响因素。其次第二特征重要度是就业人数，就业人数的增加通常反映了经济的活力和稳定性，有助于家庭形成和养育子女。稳定的就业环境不仅提升了家庭的经济保障，也增强了人们的生育意愿。