1. 引言

时间序列预测是零售、能源、金融、医疗保健、气候科学等各个领域决策的重要组成部分。传统上，预测主要使用 ARIMA 和 ETS 等统计模型。至少在最近转向深度学习技术之前，这些模型一直是可靠的工具。这一转变可归因于大量、多样的时间序列数据源的可用性，以及业务预测问题的出现，这些都发挥了深度预测的优势，即从大量时间序列集合中提取模式的能力。

预测下一个标记的语言模型和预测下一个值的时间序列预测模型之间的根本区别是什么？语言模型中的词语是来自有限词典的标记；时间序列模型中是来自连续域且无界的值，尽管他们存在明显的区别，但这两种模型从根本上都旨在对数据的顺序结构进行建模以预测未来模式。所以，好的语言模型当然可以预测时间序列！

我们基于Huggingface上的Chronos时间序列模型进行时间序列预测分析，这是一个最低限度适用于时间序列预测的语言建模框架。Chronos通过对实际值进行简单的缩放和量化，将时间序列标记为离散的Token。通过这种方式，我们可以在这种“时间序列语言”上训练现成的语言模型，而无需更改模型架构。我们基于EPS数据平台对12组数据进行了全面评估，测试结果基本超越了传统的ARIMA模型。值得注意的是，基于大语言的Chronos模型实现了令人印象深刻的开箱即用的零样本预测性能，无需针对特定任务进行调整。

2. 方法

Chronos是一个将现有语言模型架构和训练程序适用于概率时间序列预测的框架。虽然语言和时间序列在本质上都是连续的，但它们在表示形式上有所不同-自然语言由有限词汇表中的单词组成，而时间序列则是实值。这种区别要求对现有的语言建模框架进行特定的修改，特别是在标记化方面，以使其适用于时间序列数据。尽管如此，由于现有的转换器模型在语言任务中表现出色，我们的设计理念是对模型架构和训练过程进行最小限度的修改。

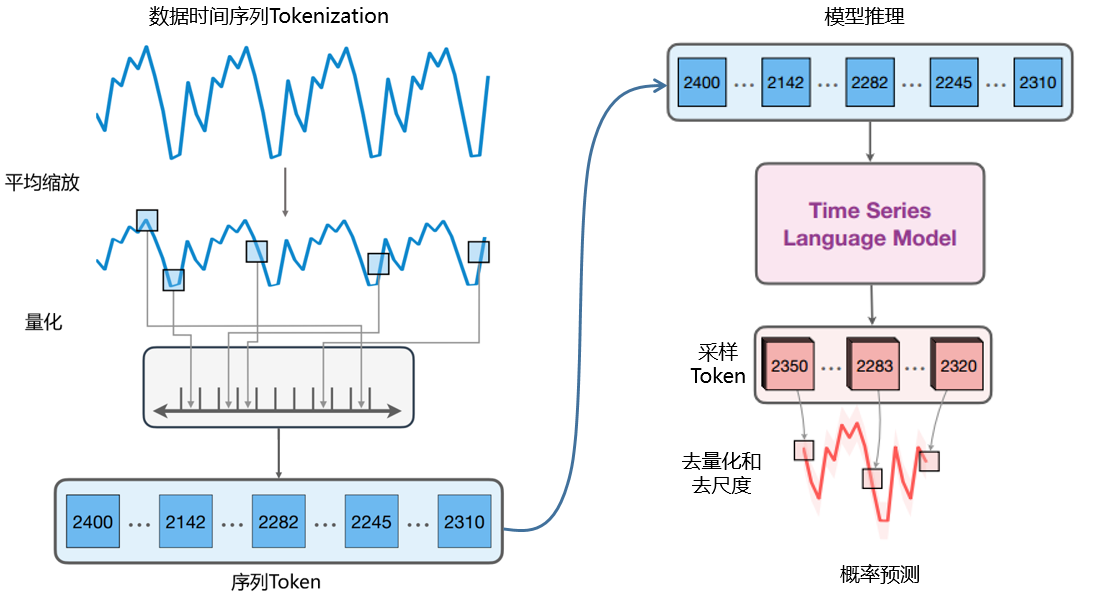
图 2-1 时间序列预测模型架构

2.1    时间序列token

考虑一个时间序列 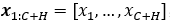 ，其中我们称前C个时刻的数据为历史的可观测数据，其余H代表模型要预测的时间范围。我们首先对观察结果进行缩放，然后将其量化为固定数量的数据token。

即使在单个数据集内，时间序列的尺度也可能存在显著差异。这对深度学习模型的优化提出了挑战。因此，对单个时间序列进行归一化，以便更好地进行优化。在Chronos中，规范化的目标是将时间序列值映射到适合量化的范围。一种常见的归一化技术包括对时间序列进行仿射变换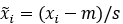。几种流行的归一化方案，如平均缩放、标准缩放和最小-最大缩放，可以通过适当选择m和s来获得。我们选择平均缩放，这是一种在实际时间序列应用中常用的深度学习模型中被证明有效的方法。平均缩放通过历史背景下绝对值的平均值对时间序列中的单个条目进行标准化。具体来说，这涉及到设置。

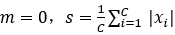归一化后的时间序列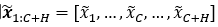，仍然是实值，不能由语言模型直接处理。为了将这些实值转换成离散的符号，我们使用了量化。形式上，我们在实际值中选择B个中心点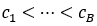，使用B-1个边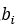分开他们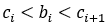其中，。量化函数为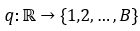：，去量化函数为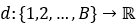，定义如下：

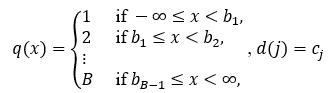
中心和边缘的定位可以是数据相关的，也可以是均匀的。分位数分类是一种数据依赖分类，它利用训练数据点的累积分布函数来构建分类箱，使得每个分类箱分配大约相等数量的数据点。

2.1    目标函数

作为典型的语言模型，我们使用分类分布作为输出分布，p(zC+h+1|z1:C+h)，其中z1:C+h是标记化的时间序列。Chronos被训练成最小化量化的真实值标签分布和预测分布之间的交叉熵。

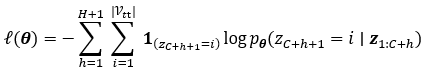
在公示中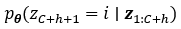表示由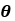参数化的模型预测的分类分布。在实践中，损失是在训练期间的一批时间序列上平均的。注意，分类交叉熵损失不是距离感知目标函数，也就是说它没有明确地识别bi比bi + 2更接近bi + 1。相反，该模型将基于训练数据集中的bi索引分布，将附近的bi关联在一起。

2.3    预测

Chronos模型是根据概率来进行预测的，对于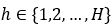，从预测分布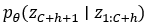中自回归采样可以得到未来多个时刻的预测值。这些预测值以token_id的形式出现，需要将其映射回实际值，然后缩放以获得实际预测。去量化函数d将预测的token_id映射到实际值：然后通过应用逆缩放变换来取消缩放，在平均缩放的情况下，该变换涉及将值乘以尺度s。

3.  数据处理

我们基于EPS数据平台，选取了人均国内生产总值、全体居民消费水平、农业机械总动力、客运量总计等六个方面的年度时间序列数据；选取了城镇居民可支配收入、房地产企业收入、价格指数等六个方面的季度时间序列数据。两种不同类型的时序数据来验证基于大语言模型的时间序列预测方法的有效性。

（1）缺失值处理：在选取的数据中，有一些年份或者季度的数据是缺失的，所以我们使用python中的interpolate方法进行插值将缺失值填充。

（2）量纲化：考虑我们需要测试多组数据，不同类型的数据之间的单位会导致两极分化（例如人均生产总值和增长率大小），但时间序列的预测，与单位无关，我们只需在评价模型时采用无量纲化的评价指标MAPE。

（3）数据质量：无论是传统的 ARIMA 模型还是深度学习模型，在数据出现急剧变化或转折时，预测往往会变得极不准确。因此，我们需要对所有数据集进行质量检测，以减少因数据异常导致的模型预测误差。如下图所示，在2012年客运量骤降，其原因公路客运量统计口径发生变化，会影响模型的预测。

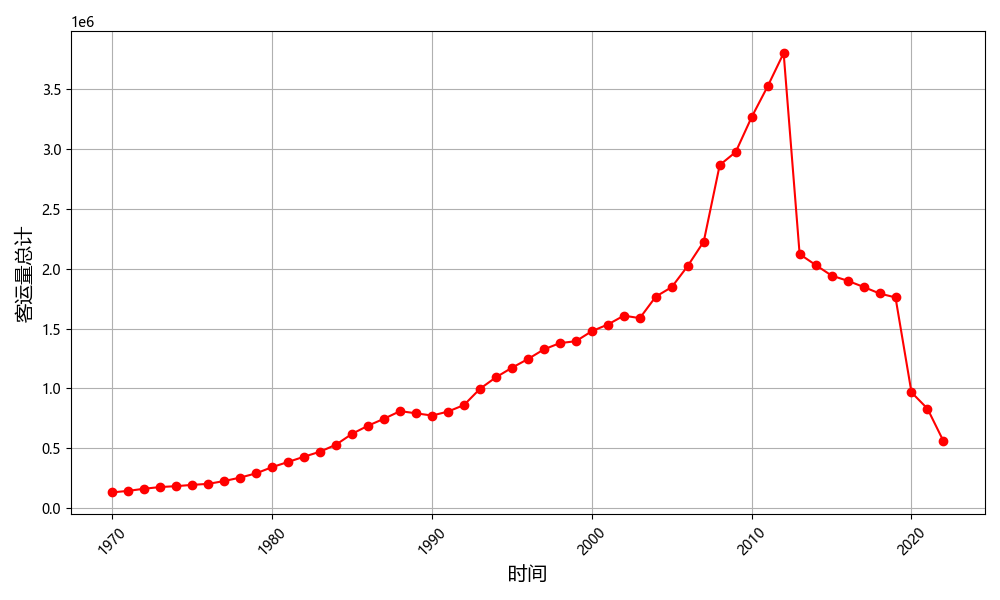
图 3-1 1970-2022年全国客运量总计

4.  结果

表 4-1 数据集测试指标分类

由于不同数据集存在量纲差异，MAPE 不受数据绝对值大小的影响（与原始数据的单位无关），因此适用于不同尺度的数据集。该指标计算预测值与真实值之间的绝对误差相对于真实值的百分比。相比于绝对误差（如均方误差 MSE），MAPE 在不同数据集之间具有更高的可比性。通过计算每个数据点的百分比误差并求平均，MAPE 提供了一个直观的整体误差量度，即平均误差的百分比。其计算公式为：

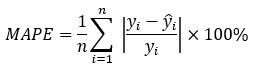
我们在选取的数据集上进行预测，为了展现模型的鲁棒性，将每个数据集设置为可观测集和不可观测集，比例为8:2。我们测试了12组数据，其中6组为季度性时间序列数据，6组为年度时间序列数据。

4.1    年度时间序列预测

我们将Chronos和ARIMA模型进行对照实验，结果如下表所示：

表 4-2 Chronos模型与ARIMA模型的年度时序预测误差

Chronos在大多数指标上优于 ARIMA，尤其在误差较大的序列上（如S5），Chronos表现更为稳定且具有较低的误差。可能由于Chronos模型结构中包含更多用于捕捉时间序列复杂模式的机制，使其在多个维度的时间序列上表现出更好的泛化能力。而ARIMA在序列S2上效果更优，可能因其经典模型在较平稳的数据上表现较好。

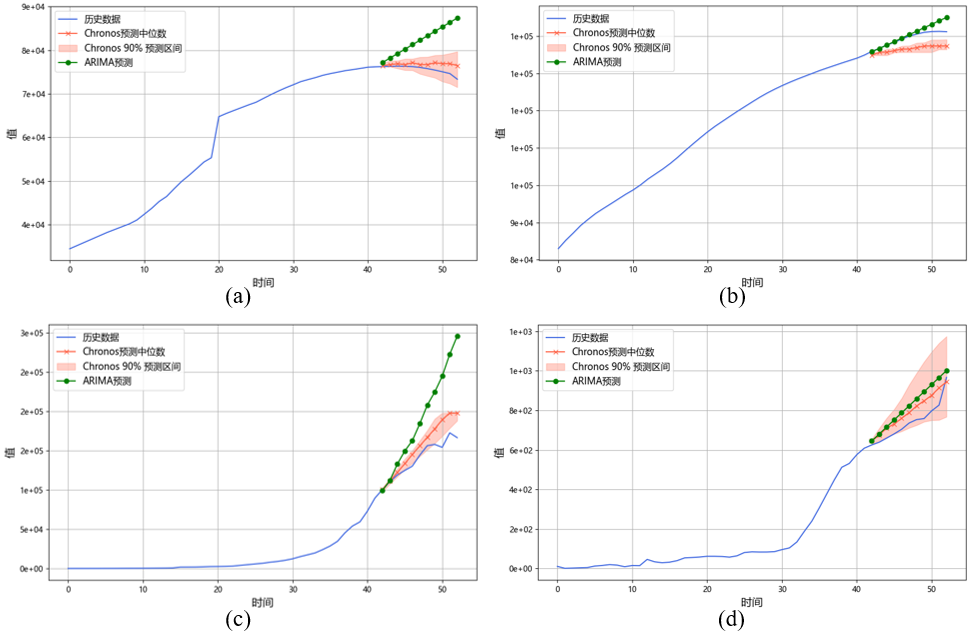
我们挑选其中四组年度时间序列：S3、S2、S5、S1、S4、S6分别进行可视化分析，对应图4-1中的（a）、（b）、（c）、（d）、（e）、（f）。

（e）                                                                      （f）

图 4-1 Chronos模型与ARIMA模型年度序列预测

Chronos 作为一个现代的深度学习模型，可能在捕捉复杂的非线性模式方面表现更好，而 ARIMA 作为经典模型，适用于线性时间序列数据。从图中分析，Chronos 模型在所提供的数据集上更准确预测未来一段时间的状态。在图（a）、（c）中，Chronos模型预测趋势稍缓和，更加接近真实状态；而在图（d）中，ARIMA模型和Chronos模型预测的结果旗鼓相当，与真实值具有相同的趋势，这说明传统ARIMA模型的预测仍然具有优势。

4.2    季度时间序列预测

在季度数据预测的评估中，对比了ARIMA模型与 Chronos 深度学习模型在各季度的表现（S7 至 S12）。评估指标显示，Chronos 模型在大多数季度的误差均低于 ARIMA 模型，特别是在 S7、S8、S10 和 S11 季度的预测中，Chronos 模型的表现明显优于 ARIMA，误差值分别为 0.052、0.023、0.050 和 0.025，体现出更好的预测精度。

表 4-3 Chronos模型与ARIMA模型的季度时序预测误差

       然而，在 S9 和 S12 季度，虽然 Chronos 模型的误差略低于 ARIMA，但两者之间的差距不大，表明 ARIMA 在这些季度的表现较为接近 Chronos。尤其在S10季度，ARIMA的误差达到0.931，显著高于Chronos的 0.050，这说明ARIMA在应对较大变化或波动的情况下效果不佳，而 Chronos 能更好地适应这些变化。总体而言，Chronos模型在大多数季度中表现出更稳定的预测能力，而ARIMA的表现则更易受季度变化的影响。

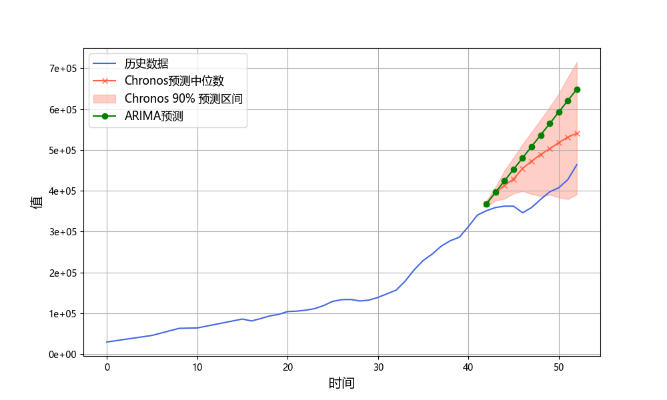
我们挑选其中四组年度时间序列：S11、S10、S7、S12、S8、S9分别进行可视化分析，对应图4-2中的（a）、（b）、（c）、（d）、（e）、（f）。

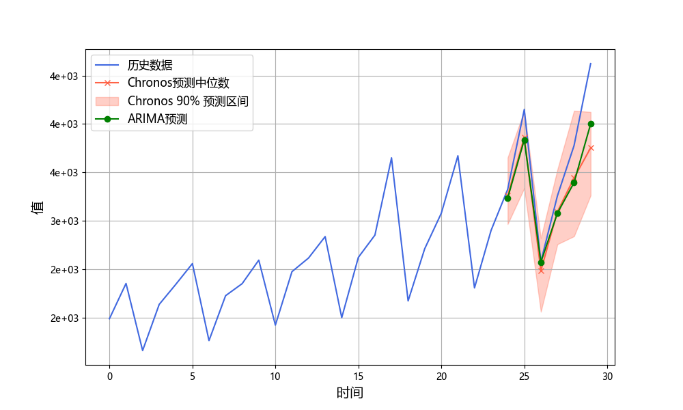
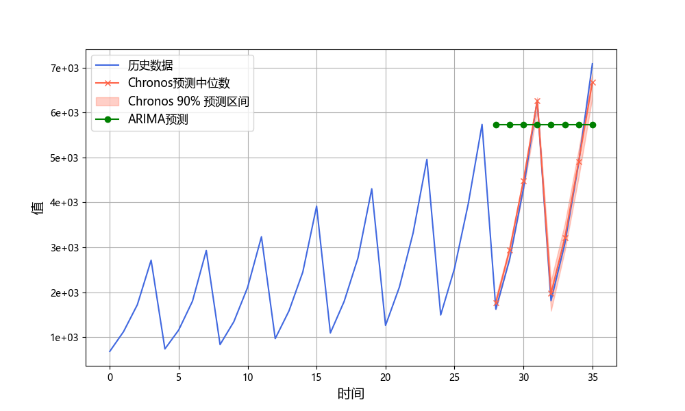
图 4-2 Chronos模型与ARIMA模型季度序列预测

通过分析季度时间序列预测图，（a）中展示了Chronos 模型和 ARIMA 模型的预测在未来时间段内均能较好地跟随实际数据的趋势。Chronos 模型的预测区间（红色阴影部分）相对较窄，表明模型对未来走势的置信度较高，且中位数预测曲线（红色线）与 ARIMA 模型（绿色线）较为接近，但 Chronos 的预测略优，尤其在误差控制上表现更好。在（b）中，Chronos 模型对数据变化的适应能力较强，但由于该数据集存在显著的波动或异常点，ARIMA 模型未能准确预测趋势，导致误差较大。Chronos 模型的预测区间能够覆盖部分数据波动，显示出对变化的适应性，但区间较宽，说明模型在置信度上有所降低。在（c）Chronos 模型在此数据集上的预测表现依然优于 ARIMA。其预测中位数紧跟真实数据走势，而 ARIMA 模型预测偏离实际趋势，尤其在后期的时间段表现较差。Chronos 模型的置信区间相对较窄，显示出较高的准确性和稳定性。在（d）中Chronos 模型的中位数预测与实际趋势保持一致，并且置信区间能够包容未来的真实数据点，表现出较好的泛化能力。相比之下，ARIMA 模型的预测误差较大，明显偏离真实数据。

从这组图表可以看出，Chronos 模型在处理复杂的时间序列数据（尤其是具有波动性或趋势性的数据）时表现更为稳健，其置信区间覆盖性较好，并且在预测精度上优于 ARIMA 模型。ARIMA 模型在某些数据集上能够捕捉基本趋势，但在数据波动较大时预测能力下降明显。Chronos 模型的较窄的置信区间也表明它对未来走势的高置信度，使其在不同数据集上具有更强的适应性和预测性能。

5.  结论

通过对年度和季度时间序列数据的实验对比分析，Chronos模型在绝大多数情况下表现出优于ARIMA模型的预测性能，尤其在数据波动大或存在复杂模式的情境下，Chronos的预测误差较低，置信区间较窄，显示出更高的预测精度和对未来趋势的置信度。这可能归因于Chronos模型结构中捕捉复杂时间序列模式的机制，使其能够在多维度数据上展现出较强的泛化能力。

在年度预测中，Chronos在大多数指标上误差较小，特别是在误差较大的序列（如S5）上表现得更为稳定，这表明Chronos模型在复杂模式的预测中具有显著优势。然而，对于较平稳的数据，ARIMA模型仍然保持较好的效果，如在S2上ARIMA的表现略优，体现出经典线性模型在简单数据集上的优势。

在季度预测中，Chronos模型同样表现出较为稳定的预测能力，当数据中存在较大波动时，Chronos模型的误差控制依旧优于ARIMA，且能够通过较窄的置信区间准确覆盖实际趋势，体现出其更高的可靠性和预测精度。

总体而言，基于大语言模型的Chronos模型在不同类型的时间序列数据中均展现出更强的适应性和预测性能，尤其适用于具有波动性或复杂模式的时间序列数据。相比之下，ARIMA模型在较平稳的时间序列上表现良好，但在数据波动较大时预测能力明显下降。因此，Chronos作为一种现代深度学习模型，在处理复杂时间序列数据方面具有显著优势，是传统时间序列模型ARIMA的有效补充和增强。