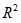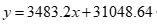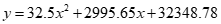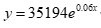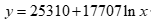2023-10-18来源:EPS数据
电力行业是保障国民经济发展的重要源泉,2021年是“十四五”规划的开局之年,也是碳达峰、碳中和“双碳”目标落地实施的第一年。在复杂的形势下,我国国民经济稳步恢复,当年全社会用电量达83313亿千瓦时,较2020年增长了10.35%,是2012年之后同比增速首次超过10%的一年。但在“十三五”期间,全国各地大规模的煤电建设高潮引发了严重的产能过剩问题,因此如何根据用电量合理规划发电量,使供需达到平衡,是一个亟待解决的问题。基于此,本文根据用电量的历史数据选择多种方法来预测未来几年的用电量,希望预测数值可以给当年的发电量提供一个参考,避免产能过剩问题。首先从发电量、用电量和发电装机容量三个方面出发,分析我国电力的发展趋势,然后基于灰色系统预测模型、趋势分析法和组合预测模型对我国的用电需求进行预测。
1、电力发展现状
1.1 发电量发展现状
2021年,我国电力行业高质量发展取得新的进展,共发电83959亿千瓦时,较2020年增加7695亿千瓦时,同比增长率达10.09%,为2011年以来的新高。其中,水能、风能、太阳能这些绿色电力发电量为23227亿千瓦时,绿色电力发电量占发电总量的比重从2008年的16.78%上升至2021年的27.66%。核电、风电、太阳能发电量逐年增加,分别从2011年的872亿千瓦时、741亿千瓦时、6亿千瓦时快速增长至4075亿千瓦时、6558亿千瓦时、3270亿千瓦时,特别是风电和太阳能发电量增长极为迅速,年均增速分别高达24%和87.8%。火电发电一直处于主导地位,但占全国发电量的占比呈缓慢下降趋势,从2008年的81.22%下降到2021年的67.48%。
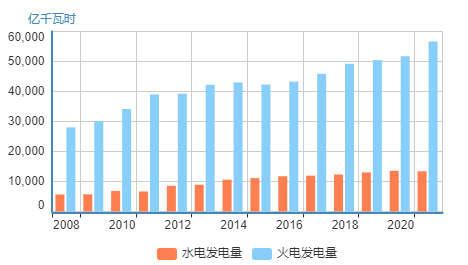
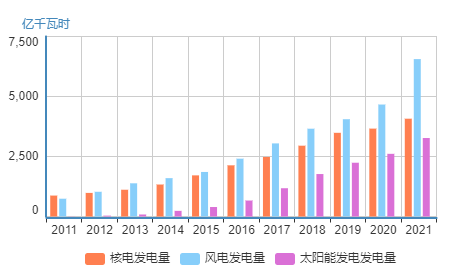
图1 2008-2021年中国不同方式发电量变化
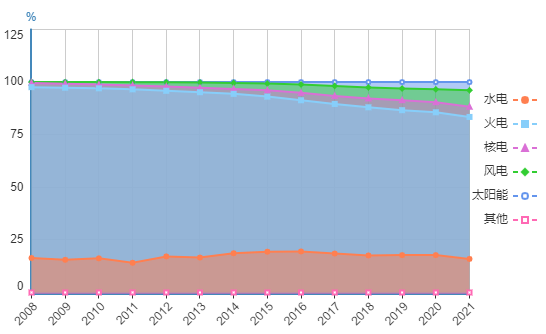
图2 2008-2021年中国发电量结构变化
1.2 用电量发展现状
2008-2021年间我国全社会用电量由34379.69亿千瓦时增长至83313亿千瓦时,共增长1.42倍,平均每年增长7.05%。“十二五”期间全社会用电量年均增速为6.3%,进入“十三五”后,全社会用电总量持续上升,但增速放缓,年均增长率为5.8%。2021年用电量的同比增速为10.35%,较发电量的增速更高。
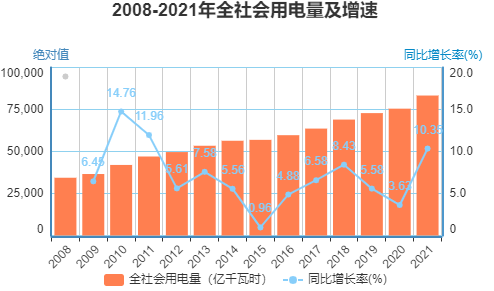
图3 2008-2021年全社会用电量及增速情况
1.3 发电装机容量
2021年,我国发电总装机容量为237777万千瓦,与2010年相比增加了141136万千瓦,增长146%。其中,火电装机容量持续上升,从2010年的70967万千瓦增长至129739万千瓦,但占比持续下降,由2010年的73%下降到2021年的54.6%。而风能、太阳能发电装机容量均增长迅速,太阳能发电装机容量从2011年的212万千瓦增加到30654万千瓦,年均增长64%;风能发电装机容量从2011年的4623万千瓦增加到32871万千瓦,年均增长21.7%。水电装机容量绝对值一直在增加,但是占比呈小幅下降趋势,从2011年的22%下降到16.4%。核电装机容量占比相对稳定,近几年一直维持在2.2%左右。
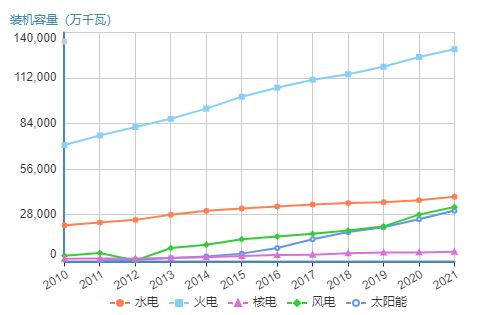
图4 2010-2021年我国电力装机容量变化
表1 2011年和2021年电源装机结构
2011年 | 2021年 | |||
装机容量(万千瓦) | 占比(%) | 装机容量(万千瓦) | 占比(%) | |
水电 | 23298 | 21.93% | 39094 | 16.44% |
火电 | 76834 | 72.31% | 129739 | 54.56% |
核电 | 1257 | 1.18% | 5326 | 2.24% |
风电 | 4623 | 4.35% | 32871 | 13.82% |
太阳能 | 212 | 0.20% | 30654 | 12.89% |
可以发现,风电、太阳能这些清洁电力正逐步实现对传统火电的替代。而不论从绝对规模还是所占比重来看,太阳能发电的发展速度都尤为迅猛,是未来发电的主力来源。
2、用电需求预测
2.1 基于灰色系统预测
灰色预测模型可以通过少量的、不完全的信息,建立数学模型并做出预测,是处理小样本预测问题的有效工具。由于用电量受多种不确定因素的影响,且当前只有2008-2021年的全社会用电量,数据量较少,属于小样本预测问题,所以可以利用灰色预测模型进行预测。
2.1.1 GM(1,1)模型
GM(1,1)模型是灰色系统的核心模型,应用广泛。核心是通过对已知序列数据进行累加构造来制造规律,并利用常微分方程和最小二乘法来求解拟合的新序列。GM(1,1)模型的建模步骤如下:
(1)级别检验
对于给定的一组数据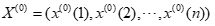 ,为了保证建立GM(1,1)模型的可行性,需要对原始序列数据进行级别检验。计算序列数据的级比
,为了保证建立GM(1,1)模型的可行性,需要对原始序列数据进行级别检验。计算序列数据的级比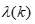 :
:
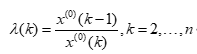
若所有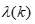 都落在区间
都落在区间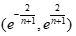 内,则可进行灰色预测;否则需要对序列数据进行平移变换,使级比落在区间内;若平移变换也无法使级比落在区间内,则说明该序列不适用GM(1,1)模型预测。
内,则可进行灰色预测;否则需要对序列数据进行平移变换,使级比落在区间内;若平移变换也无法使级比落在区间内,则说明该序列不适用GM(1,1)模型预测。
(2)GM(1,1)建模
给定一组数据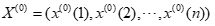 ,构造累加序列:
,构造累加序列: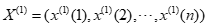 ,其中
,其中
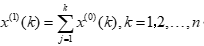
为了减小单个样本数据的波动误差,对累加序列的相邻两项数据求均值生成紧邻均值序列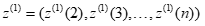 ,其中
,其中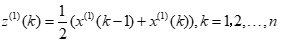 ,
,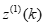 被称为白化背景值。则GM(1,1)模型的灰微分方程为:
被称为白化背景值。则GM(1,1)模型的灰微分方程为:
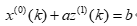
其中,a称为发展系数,用于衡量样本数据的走向趋势,b称为灰作用量。建立灰微分方程的白化方程:
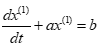
根据最小二乘法求解参数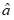 、
、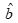 ,然后代回到白化方程中,计算得到
,然后代回到白化方程中,计算得到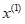 的灰色预测值为:
的灰色预测值为:
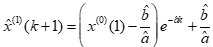
则原始序列的预测值为
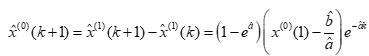
(3)精度检验
为了验证样本数据使用GM(1,1)模型的预测精度,需要进行检验。采用相对误差和后验差检验法来检验。
相对误差首先要计算残差, 即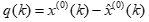 ,然后根据残差计算每组真实值和预测值的相对误差:
,然后根据残差计算每组真实值和预测值的相对误差: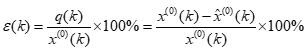 ,最后计算平均相对误差:
,最后计算平均相对误差: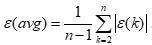 。若
。若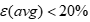 ,则该模型对原始数据的拟合效果一般;若
,则该模型对原始数据的拟合效果一般;若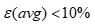 ,则该模型对原始数据的拟合效果较好。
,则该模型对原始数据的拟合效果较好。
后验差检验是计算残差序列方差和原始序列方差的比值,所得结果称为均方差比值,当该比值小于0.35时,精度等级为“好”;位于区间(0.35,0.5]时,精度等级为“合格”;位于区间(0.5,0.65]时,精度等级为“勉强”;大于0.65时,精度等级为“不合格”。
2.1.2 用电量GM(1,1)模型结果
根据用电量数据,首先计算级别比。级别比应介于区间[0.875, 1.133],原始数据并没有通过级比检验,因此进行平移转换,在原始值的基础上加入平移转换值83300,最终平移转换后的数据级比检验值均在标准范围区间[0.875, 1.143]内,意味着本数据适合进行GM(1,1)模型构建。
表2 GM(1,1)模型级比值
时间 | 原始值 | 级比值 | 平移转换后的值 | 转换后的级比值 |
2008年 | 34379.690 | - | 117679.69 | - |
2009年 | 36598.420 | 0.939 | 119898.42 | 0.981 |
2010年 | 41999.000 | 0.871 | 125299 | 0.957 |
2011年 | 47022.000 | 0.893 | 130322 | 0.961 |
2012年 | 49658.000 | 0.947 | 132958 | 0.980 |
2013年 | 53423.000 | 0.930 | 136723 | 0.972 |
2014年 | 56393.000 | 0.947 | 139693 | 0.979 |
2015年 | 56933.000 | 0.991 | 140233 | 0.996 |
2016年 | 59710.000 | 0.953 | 143010 | 0.981 |
2017年 | 63636.000 | 0.938 | 146936 | 0.973 |
2018年 | 69002.000 | 0.922 | 152302 | 0.965 |
2019年 | 72852.000 | 0.947 | 156152 | 0.975 |
2020年 | 75498.000 | 0.965 | 158798 | 0.983 |
2021年 | 83313.000 | 0.906 | 166613 | 0.953 |
根据GM(1,1)模型的建模步骤,得到模型的基本参数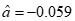 ,
,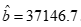 .则预测模型为:
.则预测模型为: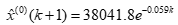 。据此可以计算出2008-2021年我国全社会用电量的灰色预测值,对比历史数据进行预测误差及精度检验,结果如表3、表4所示。该模型的平均相对误差为2.54%,2009年的相对误差较大,为9.31%,其余年份都小于5%。模型的均方差比为0.0938,对比精度检验等级参照表5可知,该模型对历史数据的拟合精度很好。
。据此可以计算出2008-2021年我国全社会用电量的灰色预测值,对比历史数据进行预测误差及精度检验,结果如表3、表4所示。该模型的平均相对误差为2.54%,2009年的相对误差较大,为9.31%,其余年份都小于5%。模型的均方差比为0.0938,对比精度检验等级参照表5可知,该模型对历史数据的拟合精度很好。
表3 GM(1,1)模型预测误差检验
时间 | 真实值 | 预测值 | 相对误差(%) |
2008年 | 34379.69 | 34379.69 | 0.00 |
2009年 | 36598.42 | 40357.60 | 9.31 |
2010年 | 41999.00 | 42813.25 | 1.90 |
2011年 | 47022.00 | 45418.32 | 3.53 |
2012年 | 49658.00 | 48181.91 | 3.06 |
2013年 | 53423.00 | 51113.65 | 4.52 |
2014年 | 56393.00 | 54223.78 | 4.00 |
2015年 | 56933.00 | 57523.16 | 1.03 |
2016年 | 59710.00 | 61023.29 | 2.15 |
2017年 | 63636.00 | 64736.40 | 1.70 |
2018年 | 69002.00 | 68675.44 | 0.48 |
2019年 | 72852.00 | 72854.16 | 0.00 |
2020年 | 75498.00 | 77287.14 | 2.31 |
2021年 | 83313.00 | 81989.86 | 1.61 |
表4 GM(1,1)模型预测精度分析
平均相对误差Q | 均方差比C |
2.54% | 0.0938 |
表5 精度检验等级参照表
模型精度等级 | 均方差比值 |
好 | C<=0.35 |
合格 | 0.35<=C<=0.5 |
勉强合格 | 0.5<=C<=0.65 |
不合格 | 0.65<C |
利用得到的GM(1,1)模型对我国2022-2029年间的用电需求进行预测,结果如图5.预测结果表明到2025年我国全社会用电量将达到10.38万亿千瓦时,2029年达到13.15万亿千瓦时。
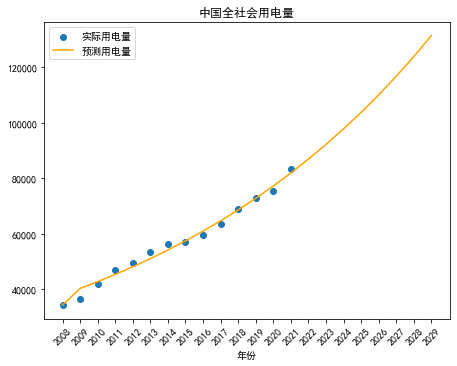
图5 基于GM(1,1)模型的用电需求预测
2.2 基于趋势分析法
趋势分析法是将不同时期数据中的相同指标或比率进行比较,直接观察其增减变化或变动幅度,考察其发展趋势,预测发展前景。常见的趋势预测法函数模型有:
(1) 直线模型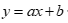
(2) 二次曲线模型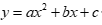
(3) 指数曲线模型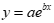
(4) 对数曲线模型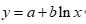
对2008-2021年我国全社会用电量数据分别构建上述4种模型进行拟合,并计算决定系数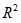 来评估模型的拟合程度,该值越接近1,说明模型的拟合程度越好。从表6可知,二次曲线模型的拟合效果最好。
来评估模型的拟合程度,该值越接近1,说明模型的拟合程度越好。从表6可知,二次曲线模型的拟合效果最好。
表6 不同函数模型的拟合结果
函数模型 | 拟合结果 |
|
直线模型 |
| 0.9856 |
二次曲线模型 |
| 0.9867 |
指数曲线模型 |
| 0.9825 |
对数曲线模型 |
| 0.8722 |
表7 二次曲线模型预测误差检验
时间 | 真实值 | 预测值 | 相对误差(%) |
2008年 | 34379.69 | 35376.931935 | 2.82 |
2009年 | 36598.42 | 38470.092638 | 4.87 |
2010年 | 41999.00 | 41628.260042 | 0.89 |
2011年 | 47022.00 | 44851.434146 | 4.84 |
2012年 | 49658.00 | 48139.614950 | 3.15 |
2013年 | 53423.00 | 51492.802454 | 3.75 |
2014年 | 56393.00 | 54910.996659 | 2.70 |
2015年 | 56933.00 | 58394.197563 | 2.50 |
2016年 | 59710.00 | 61942.405168 | 3.60 |
2017年 | 63636.00 | 65555.619474 | 2.93 |
2018年 | 69002.00 | 69233.840479 | 0.33 |
2019年 | 72852.00 | 72977.068185 | 0.17 |
2020年 | 75498.00 | 76785.302591 | 1.68 |
2021年 | 83313.00 | 80658.543698 | 3.29 |
用二次曲线模型建模,误差检验结果如表7所示。该模型的平均相对误差为2.68%,最大误差为4.87%,故认为该模型具有很好的预测效果。利用该模型进行预测,结果如图6.预测结果表明到2025年我国全社会用电量将达到9.68万亿千瓦时;2029年达到11.40万亿千瓦时。
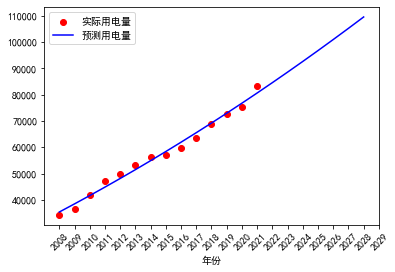
图6 基于二次曲线模型的用电需求预测
2.3 基于组合预测模型
组合预测模型是根据一定的准则赋予单个单项模型一定的权重,而后根据权重组合到一起形成新的模型,能够在一定程度上弥补单一模型固有的缺陷,提高预测精度。根据前两种GM(1,1)模型和二次曲线模型构建组合预测模型,对我国的全社会用电量进行预测。
该模型权重的设定方法主要有:等权法、简单加权平均法、误差平方和倒数法等,本文选择误差平方和倒数法来设定权重。
对于第i个模型,样本内误差平方和为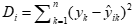 ,其中n为样本量,
,其中n为样本量,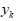 为第k期的真实值,
为第k期的真实值,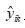 为第i个模型第k期的预测值,则该模型的权重为
为第i个模型第k期的预测值,则该模型的权重为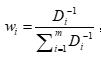 ,其中m为模型个数。
,其中m为模型个数。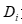 越大,第i个模型的预测误差越大,相应的权重就越小,反之亦然。
越大,第i个模型的预测误差越大,相应的权重就越小,反之亦然。
求出单个模型的权重后,建立组合预测模型:
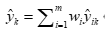
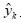 为组合预测模型第k期的预测值,
为组合预测模型第k期的预测值,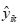 为第i个模型的预测值。
为第i个模型的预测值。
经过计算得出我国用电需求的组合预测模型为:
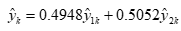
其中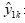 表示GM(1,1)模型,
表示GM(1,1)模型,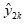 表示二次曲线模型。进行误差检验,结果如表8所示。该模型预测结果的平均相对误差为2.53%,而GM(1,1)模型和二次曲线模型的平均相对误差分别为2.54%和2.68%,可见组合预测模型提高了预测精度。
表示二次曲线模型。进行误差检验,结果如表8所示。该模型预测结果的平均相对误差为2.53%,而GM(1,1)模型和二次曲线模型的平均相对误差分别为2.54%和2.68%,可见组合预测模型提高了预测精度。
表8 组合预测模型预测误差检验
时间 | 真实值 | 二次预测值 | GM(1,1)预测值 | 组合预测值 | 相对误差(%) |
2008年 | 34379.69 | 35376.93 | 34379.69 | 34873.16 | 1.415042 |
2009年 | 36598.42 | 38470.09 | 40357.6 | 39423.6 | 7.166206 |
2010年 | 41999 | 41628.26 | 42813.25 | 42226.88 | 0.539647 |
2011年 | 47022 | 44851.43 | 45418.32 | 45137.81 | 4.174316 |
2012年 | 49658 | 48139.61 | 48181.91 | 48160.98 | 3.108365 |
2013年 | 53423 | 51492.8 | 51113.65 | 51301.27 | 4.135828 |
2014年 | 56393 | 54911 | 54223.78 | 54563.84 | 3.352333 |
2015年 | 56933 | 58394.2 | 57523.16 | 57954.18 | 1.762046 |
2016年 | 59710 | 61942.41 | 61023.29 | 61478.1 | 2.875983 |
2017年 | 63636 | 65555.62 | 64736.4 | 65141.78 | 2.31154 |
2018年 | 69002 | 69233.84 | 68675.44 | 68951.76 | 0.072869 |
2019年 | 72852 | 72977.07 | 72854.16 | 72914.98 | 0.086374 |
2020年 | 75498 | 76785.3 | 77287.14 | 77038.81 | 2.000048 |
2021年 | 83313 | 80658.54 | 81989.86 | 81331.08 | 2.436856 |
利用该组合预测模型进行预测,结果如图7.预测结果表明到2025年我国全社会用电量将达到10.03万亿千瓦时;2029年达到12.27万亿千瓦时。
表9 组合预测模型用电需求预测
时间 | 全社会用电量(亿千瓦时) | 年均增速(%) |
2022年 | 85775.46 | - |
2023年 | 90416.64 | 5.41 |
2024年 | 95250.01 | 5.35 |
2025年 | 100285.3 | 5.29 |
2026年 | 105532.7 | 5.23 |
2027年 | 111003.2 | 5.18 |
2028年 | 116708.4 | 5.14 |
2029年 | 122660.5 | 5.10 |
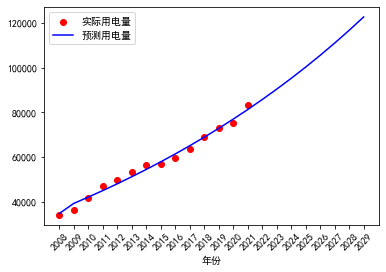
图7 基于组合预测模型的用电需求预测
3、结论
本文利用灰色系统预测模型GM(1,1)、趋势分析法和组合预测模型对我国的用电需求进行预测,经过比较,组合预测法的预测精度最高,其预测结果如表9所示。数据表明,未来我国全社会用电量将以5%以上的增速平稳上升,2025年将突破10万亿千瓦时,达到10.03万亿千瓦时;2029年达到12.27万亿千瓦时,预测结果能为电力系统实现供需平衡提供一定的参考性。