一 原理介绍

1.1 模型表达式

在介绍ARIMA之前，需要对AR模型，MA模型先进行简单的介绍，ARIMA模型则是这两个模型的进化。以下则是对于这一系列模型的介绍。

（1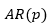）模型

AR模型的原理是使用该观测点之前时刻的观测点的线性组合来描述之后时刻的观测点的值，属于线性回归，AR模型表明，任意时刻观测点的值都取决于前边p个时刻的观测值再加上一个误差，其数学表达式如下所示。

P阶自回归模型：

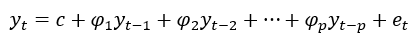
式中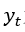，为时间序列第t时刻的观察值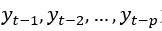，为时间序列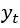的滞后时间的观察值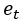，是随机误差项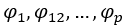，是自回归序列的待估参数。

（2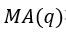）模型

MA（移动平均过程）模型，在一个q阶移动平均模型中，时序中的每个值都可以用之前的q个残差的线性组合来表示。其数学表达式如下所示。

q阶移动平均模型：

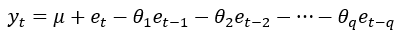
式中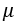，为时间序列的平均值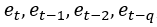，是模型的第t期，第t-1期，第t-q期的误差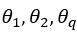，是待估参数。

（3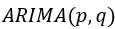）模型

自回归与移动平均结合,序列中每个观测值都可以用过去的p个观测值和q个残差值的线性组合来表示，模型的形式为：

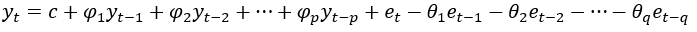
显然，从公式可以看出，该模型是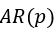和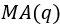的混合模型，当q=0时，退化为纯自回归模型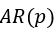，当p=0时，退化为移动平均模型。

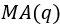（4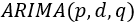）模型

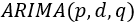模型全称为差分自回归移动平均模型.。原理是将非平稳时间序列转换为平稳时间序列。然后将因变量仅对它滞后值（阶数）以及随机误差项的现值和滞后值进行回归所建立的模型。

相比较于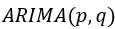模型而言，这里的d是对原序列数据进行逐期差分的阶数，差分的目的是为了使非平稳序列变换为平稳序列，通常差分的取值为0.1.2，一般的非平稳序列基本差分2阶则就会变得平稳，当差分阶数过高时，对原数据则无法有很好的解释。

（5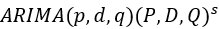）模型

对于季节性的非平稳时间序列，需要进行季节性差分才能得到平稳时间序列，这里的D是季节性差分的阶数，P,Q是季节性自回归阶数和季节性移动平均阶数，S为季节周期的长度，如果是月度数据，则S=12，如果是季度数据，则S=4。

1.2 模型识别

识别模型的方法是确定确定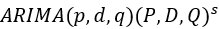模型中p,d,q以及P,D,Q和S的取值。因此我们需要借助自相关图和偏自相关图来判断模型的p和q值。

首先判断时序是否平稳，若不平稳，经过差分后平稳，则可以根据差分阶数判断D和d。p和q则可以根据自相关系数和偏自相关系数是否在某一阶截尾或者拖尾给出相应的值。

二 实例分析

随着人民生活水平的提高，旅游成为一种极好的休闲的方式，我国地域广阔，历史悠久，更有许多世界闻名的风景，近年来，来我国旅游的外国人越来越多，因此对于外国游客的人数预测，地域分布等研究也有一定的必要。

2.1 选择数据

在此我们选择2010年1月到2017年12月的月度数据，选择指标为入境外国游客人数，按地区分为亚洲，欧洲，美洲，大洋洲，非洲。我们需要对这五组数据都要预测，根据数据的特点，可以分别对这五个时间序列数据进行建模预测。

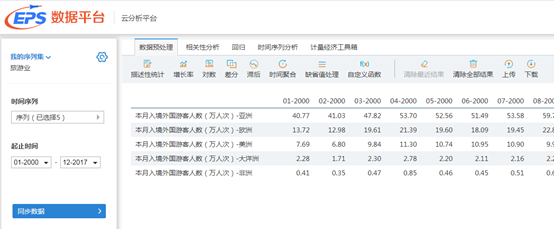
2.2 数据的可视化

可以看到，亚洲游客人数的增长趋势呈现线性，但是在2016年10月有显著的增长点，整体有一定的季节效应，但波动幅度较小；欧洲游客人数前期有上升的趋势，后期是有一定的下降趋势，波动幅度较大，有明显的季节效应；美洲游客人数呈线性增长，并有一定的季节波动效应；大洋洲游客人数前期增长加快，后期增长平缓，有一定的季节效应，非洲游客人数的呈线性增长，有明显的季节效应。

2.3 数据建模

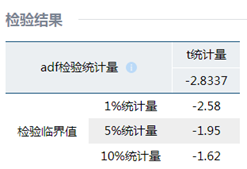
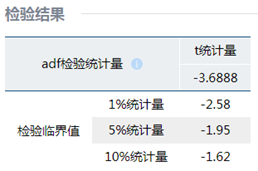
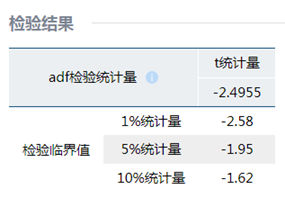
验证序列的平稳性

根据数据的可视化可以明显的看出数据为非平稳序列，因此可以对数据进行差分，由于序列都显示出季节效应，因此需要做季节性差分，然后对差分后的数据进行平稳性检验，最终结果显示，这五个一阶季节性差分序列的统计量均小于1%的临界值，因此可以认为这5个一阶季节性差分后的时间序列均为平稳序列。

选择模型

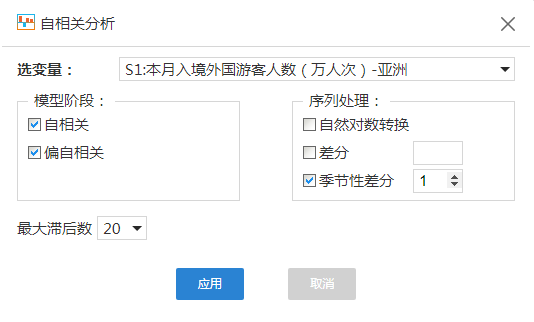
我们可以通过AFC图和PAFC图来选择备选模型，在时间序列分析的模块中有自相关分析，如图所示，我们点击自相关分析，会弹出自相关分析的对话框，在对话框中选择变量和方法，滞后阶数选择20，由于序列有典型的季节性效应，并且一阶季节性差分后的数据平稳，由于我们选择的是原序列，不是差分后的序列，因此需要在序列处理中的季节性差分中选择1阶差分。点击应用之后我们就可以得到需要的自相关图形和偏自相关图形。

（1）亚洲游客人数

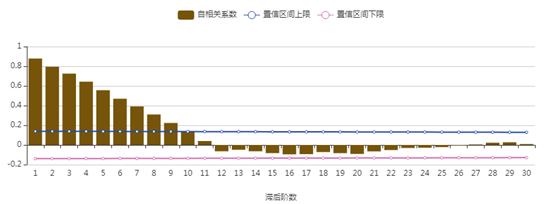
从亚洲游客人数的自相关图和偏自相关图来看，自相关系数表现为拖尾，偏自相关系数在1阶之后截尾，而偏自相关在12阶和24阶时有明显的突起，因此选择p=1,d=0,q=0,P=2,D=1,Q=0,S=12建立模型为。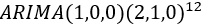

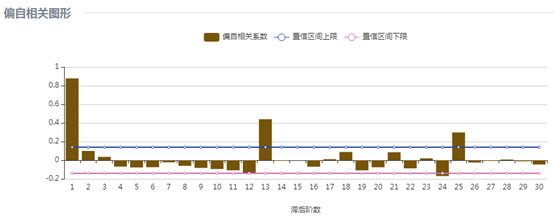
（2）欧洲游客人数

欧洲游客人数的自相关图拖尾，偏自相关图在2阶之后截尾，12阶上有一个明显的凸起，因此确定p=2,d=0,q=0,P=1,D=1,Q=0,S=12建立模型为。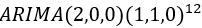

（3）美洲游客人数

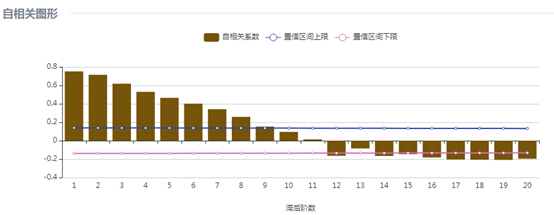
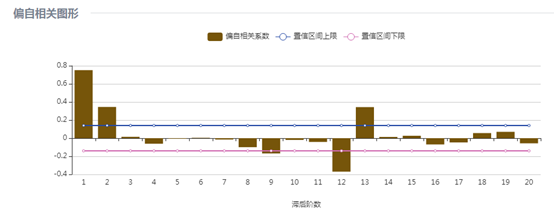
美洲游客人数的自相关图拖尾，12阶上有一个明显的突起，偏自相关图在1阶之后截尾，12阶上有一个明显的凸起，因此确定p=1, d=0, q=0, P=1, D=1,=Q=1,S=12，建立模型为。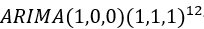

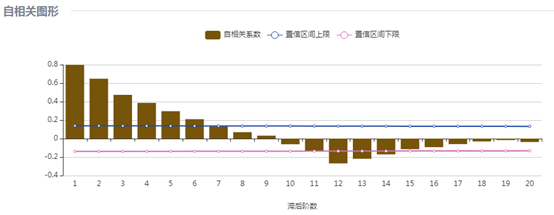
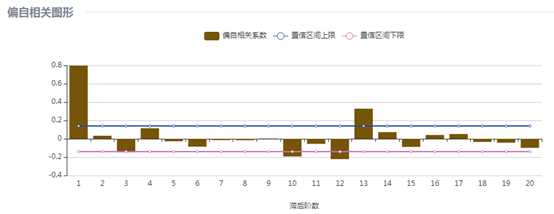
（4）大洋洲游客人数

大洋洲游客人数的自相关图拖尾，偏自相关图在1阶之后截尾，12阶上有一个明显的凸起，因此确定p=1, d=0, q=0, P=1, D=1,=Q=0,S=12，建立模型为。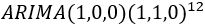

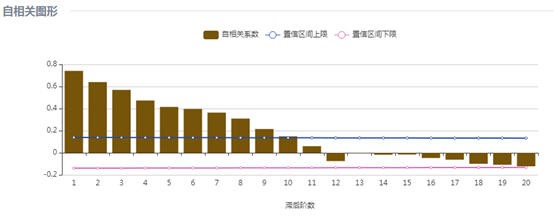
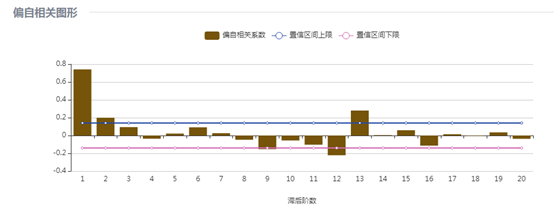
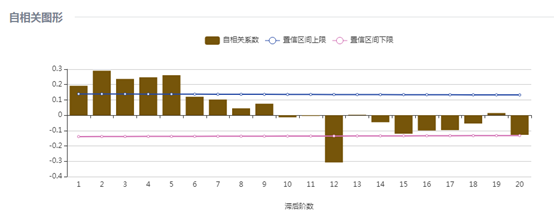
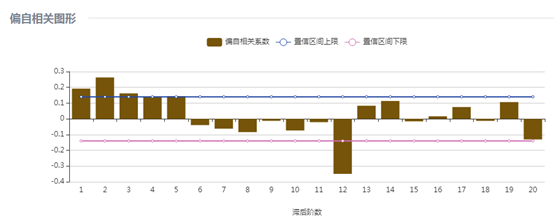
（5）非洲游客人数

非洲游客人数的自相关图在5阶之后截尾，12阶有明显突起，偏自相关图在5阶之后截尾，12阶上有一个明显的凸起，因此确定p=5, d=0, q=5, P=1, D=1,=Q=1,S=12，建立模型为。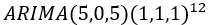

拟合模型

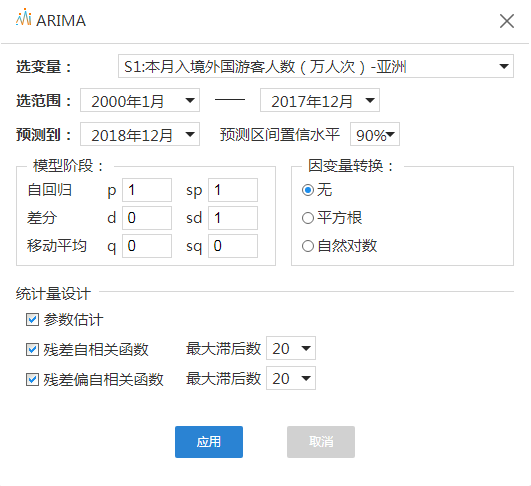
根据自相关图和偏自相关图确定了基础的模型之后，就可以建立相应的模型，点击ARIMA模型，弹出该模型的对话框，在对话框中选择时间序列以及参数，在对话框中选择内容有

选变量：选择需要预测的时间序列。

选范围：选择变量的起止时间。

预测到：选择需要预测的时间段。

模型阶段：选择模型的参数。

因变量转换：原始数据如果过大则会做一些变换使原始数据便于建模。

统计量设计：建模之后给出的模型的估计参数以及残差的结果。

我们分别对这5个序列用ARIMA建立模型，其中模型阶段的p,d,q,P,D,Q根据自相关和偏自相关给出各自不同的值，其余的选项则都一致，这些数据也不需要变形，因此因变量转换选择无，为了给出建模之后的模型评价来判断模型的拟合效果，因此统计量设计的复选款都需要选择，并且滞后阶数选择20。

模型评价

一般来说，如果一个模型合适，那模型的残差应该满足均值为0的正态分布，我们可以对残差进行自相关和偏自相关检验，若残差不存在自相关性和偏自相关性，表明拟合的模型是优良的，也可以使用Ljung-BoxQ对残差进行白噪声检验，若检验结果是白噪声，则表明模型拟合效果较好。

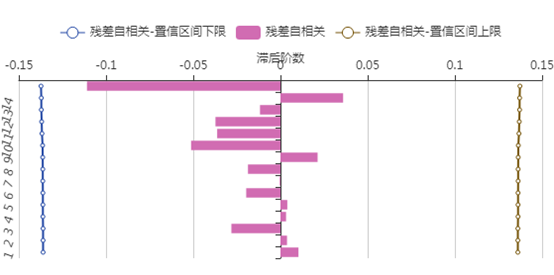
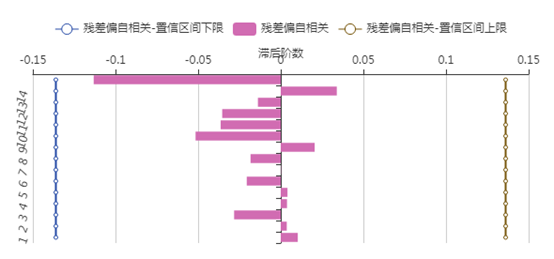
（1）亚洲游客人数的ARIMA模型

该序列选择的是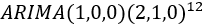模型，可以看到亚洲游客人数的残差的白噪声检验的p值为0.8598，通过了白噪声检验，并且通过残差的自相关图和偏自相关可以看到，残差的自相关图和偏自相关图不存在截尾和拖尾现象，因此可以认为残差不存在自相关和偏自相关性。

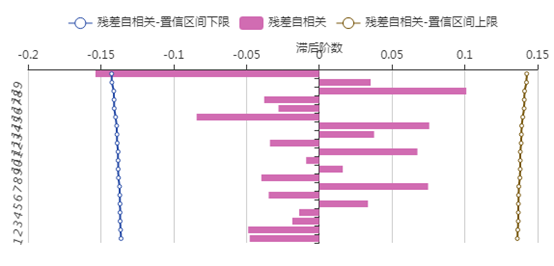
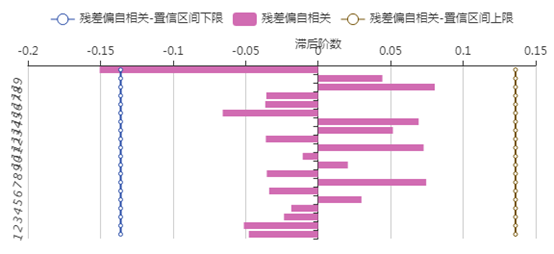
（2）欧洲游客人数的ARIMA模型

首先我们建立了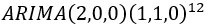的模型，同时为了作比较，选出更好的模型，因此建立了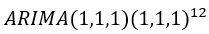模型，对比AIC，第一个模型的AIC值为1134，第二个模型的AIC值为1105，根据AIC越小模型越好的准则，最终选择。

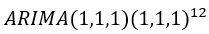从残差的检验结果来看，残差通过白噪声的检验，并且残差没有自相关和偏自相关性。因此该模型拟合很好。

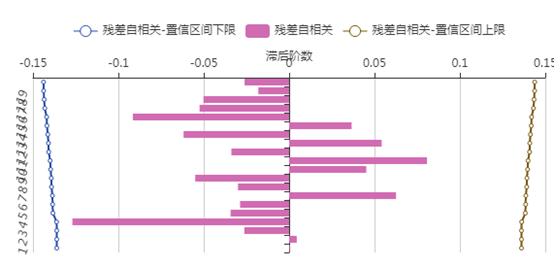
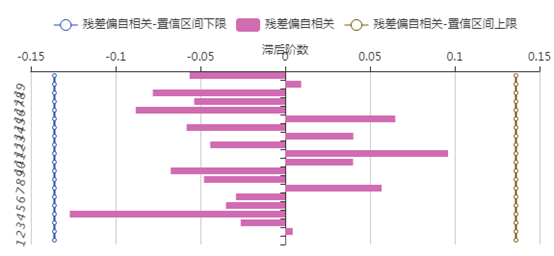
（3）美洲游客人数的ARIMA模型

同样的选择最优模型对比，最终的拟合模型为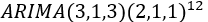，残差的白噪声检验结果为0.67，接受残差为白噪声的原假设，并且残差的自相关图和偏自相关图表明残差没有自相关性和偏自相关性，以上结果表明模型拟合很好。

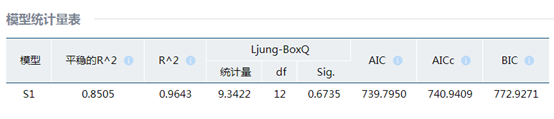
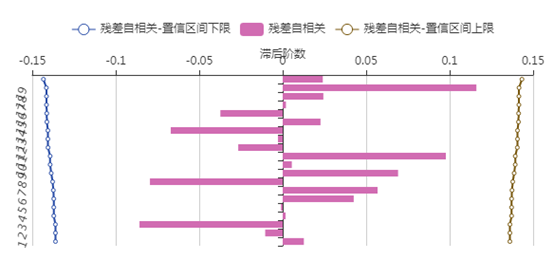
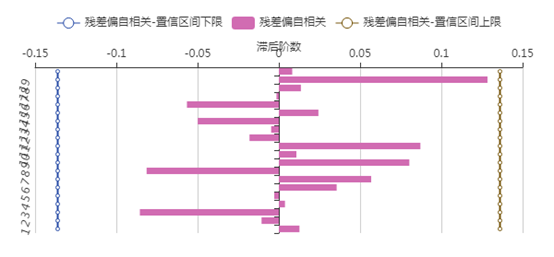
（4）大洋洲游客人数的ARIMA模型

使用的模型是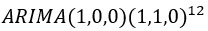，残差通过白噪声检验，并且不存在自相关和偏自相关性。

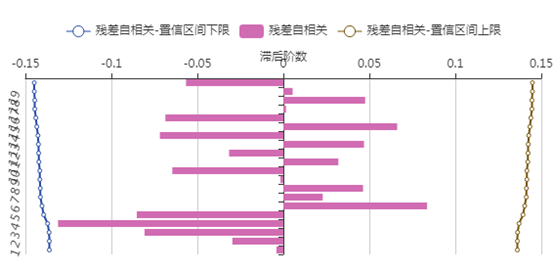
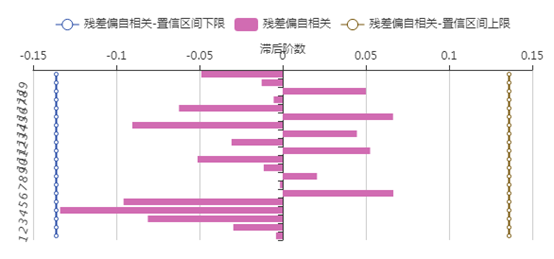
（5）非洲游客人数的ARIMA模型

最终建立的模型为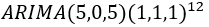，残差通过白噪声检验，并且不存在自相关性和偏自相性。

2.4 数据预测

根据最终建立的模型进行为期一年的预测，以下5个图是这五个洲的拟合预测图。

(1) 亚洲的拟合图可以看出，模型的拟合值与真实值相差不大，但是整体有一些滞后，并且2018年的预测值可以看到相对于2017年，2018年的波动幅度较大，整体保持平稳增长的趋势。

(2) 欧洲的拟合图可以看到，整体拟合效果可以，但是在峰值部分的拟合不是很好，2018年的预测值相较于2017年没有很大的波动与变化。

(3) 美洲的拟合图可以看到，2010年之前的整体拟合值较好，2010年到2014年的峰度的拟合值效果不好，但是在2014年之后，高峰的拟合值效果很好，2018年的预测值显示美洲的游客人数较为平稳。

(4) 大洋洲的拟合图可以看到2008年之前的拟合值有点滞后，2008年之后的拟合效果还可以，预测值则相较于前一年的真实值比较平稳，没有太大的波动。

(5) 非洲的拟合图可以看出，整体的拟合效果还可以，个别峰值由于变化过大所以该部分的拟合不是很好，预测值也是平稳的增长。

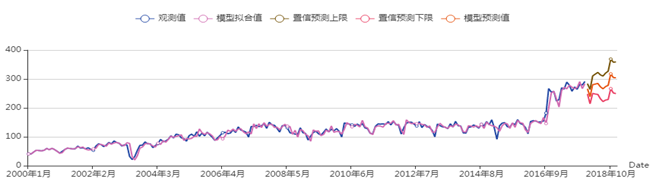
亚洲游客人数的拟合预测图

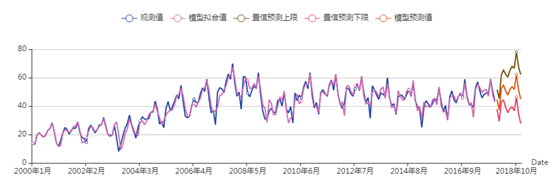
欧洲游客人数的拟合预测图

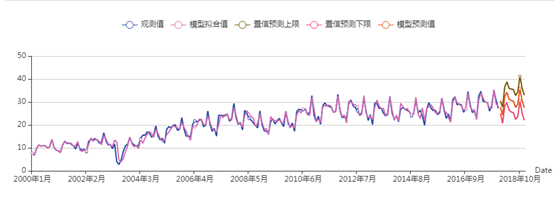
美洲游客人数的拟合预测图

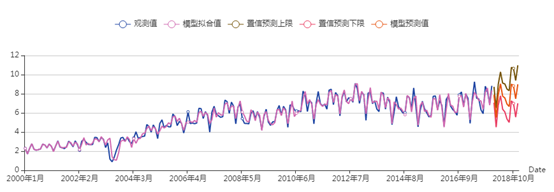
大洋洲游客人数的拟合预测图

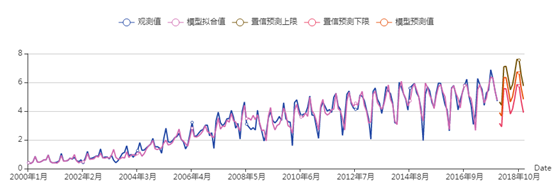
非洲游客人数的拟合预测图

中国文化和旅游部公布的2018年旅游市场数据是：入境外国游客人数4795万人次（含相邻国家边民旅华人次），亚洲占76.3%，美洲占7.9%，欧洲占12.5%，大洋洲占1.9%，非洲占1.4%。下表是五个洲的2018年旅游人数的预测值，其中亚洲占比75%，欧洲占比13.4%，美洲占比8%，大洋洲占比2%，非洲占比1.4%。其中我们的预测值低估了亚洲的旅游人数，高估了欧洲的旅游人数，其他大洲的估计结果相对较好。

表：2018年各大洲游客人数的预测结果 单位（万人次）

三 总结

我国的旅游业发展较快，其中亚洲人数占比过大，因此亚洲人数的增降直接影响我国旅游业人数的增降，而亚洲旅游人数在2016年有较大的增长，其他大洲则没有明显的增长点，究其原因可能是我国的一带一路政策引起的，因此在2018年对于亚洲的旅游人数的预估则有些偏低，而欧洲的旅游人数在2008年一直是增长的趋势，在08年之后有一定的下降趋势，因此在2018年的预测中高估了旅游人数的增长。而其他三个洲的趋势是稳定的增长，因此预测结果与真实结果相差不大。

综上，可以看到我国的旅游业发展水平很好，建立模型是为了更好的预测未来的国际旅游人数情况，为国家或者相关企业做决定提供一些依据，但是旅游业受到2020年的疫情使影响，因此在2020年的旅游人数有很大的减少，因此该模型如果用来预测2020年的人数，则会有很大的偏差，当然在未来，还可以用该模型2020年的预测值来2020年的真实值做对比，分析疫情对于旅游业发展造成的影响。最后，虽然疫情还未过去，并且旅游业还处于寒冷时期，但是相信一切都会好的。