2020-07-22来源:EPS数据平台
一 VAR模型理论介绍
VAR模型又称向量自回归模型,是一种常用的计量经济模型,该模型扩充了只用一个变量的自回归模型,是采用多方程联立的形式,不以经济理论为基础,在模型的每一个方程中,内生变量对模型的全部内生变量的滞后期进行回归,从而估计全部内生变量的动态关系,并进行预测。该模型使得时间序列分析从单一时间序列拓展到了多元时间序列,被广泛的应用在金融和经济等多个领域。可以说,只要问题涉及多变量,时间序列数据,都有可能使用VAR模型。
模型定义:以两个变量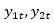 滞后1期的VAR模型为例,VAR模型可表达为:
滞后1期的VAR模型为例,VAR模型可表达为:
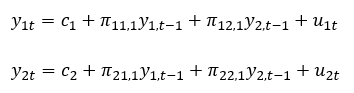
联立两个方程得到的就是VAR模型的方程形式。
写成矩阵形式如下所示:
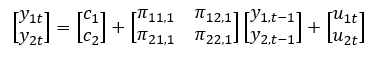
设
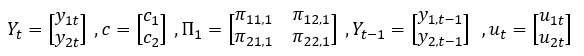
则 矩阵形式可以表示为:

二 实证分析
2.1 选取指标
准确地预测居民消费价格指数,是合理地制定宏观经济政策的前提。国内许多学者都对居民消费价格指数的预测进行了研究。在这里我们使用VAR模型进行研究预测。
在此次研究中我们选取的指标有:
居民消费价格指数(CPI)
CPI是根据与居民生活有关的产品及劳务价格统计出来的物价变动指标,通常用来作为观察通货膨胀水平的指标。
广义货币(M2)
经济学中推动物价上涨:需求拉动和成本推动。其中需求拉动分为货币因素和实际需求,货币需求指标在这里用M2表示。
人民币名义有效汇率(NEER)
我国是一个进出口贸易很大的国家,国际市场的影响对国内物价的影响也很大,因此把汇率也作为影响因素之一,由于人民币有效汇率暂时无法获得,所以选择人民币对美元的汇率。
工业生产者出厂价格指数(PPI)
工业品出厂价格指数是衡量工业企业产品出厂价格变动趋势和变动程度的指数,是反映某一时期生产领域价格变动情况的重要经济指标。
工业增加值指数(IAV)
除货币因素外,实际需求是需求拉动的另一个重要组成,国内GDP是反映在一定时期内生产出的全部最终产品和劳务的价值,其反映了国内的实际需求,但是由于没有月度的国内GDP数据,因此选择工业增加值指数作为替代变量,表示国内的净需求
农产品价格指数(API)
通货膨胀的压力也会来自食品,因此食品零售价格指数也可能是影响CPI的因素之一。
2.2 选取数据
确定了使用以上指标之后,我们从EPS数据平台中选取这些指标2005年-2019年的月度数据。如图所示,我们从中国宏观数据库选取居民价格消费指数的指标,选择添加序列,把该条指标添加到我们自定义的文件夹中,在这里,我把这次建模的文件夹定义为“VAR建模”。同样的,我们可以在EPS数据平台的中国宏观经济数据库中找到自己需要的数据添加到同一个文件夹,具体展示如下。
2.3 数据预处理
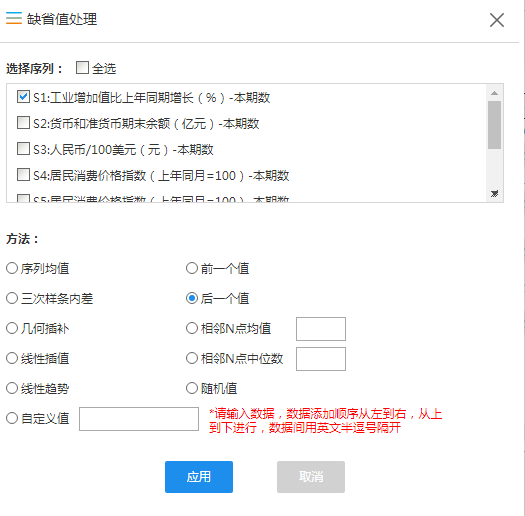
由于工业增加值指数在每年的1月份数据有缺失,因此我们采用后一个值对缺失数据进行填充。具体如下图所示。
2.4 数据平稳性检验及处理
时间序列分析模型的建模前提是数据要有平稳性,数据平稳才能进行下一步操作,因此我们对以上选取的指标先用可视化直观判断数据的平稳性,如下图所示可以看到这些指标均为不平稳序列。




原序列确定是不平稳序列,我们尝试对一阶差分后的序列进行平稳性检验,我们选择数据预处理中的差分,然后选择需要差分的6个指标,差分阶数选择1,点击确认,可以得到这6个指标的一阶差分值,我们可以直接给出这6个一阶差分序列的折线图,从图中看到数据基本都是平稳的,但是为了使得数据平稳更加有说服力,我们选择平台提供的数据平稳性检验算法来检验这6个一阶差分序列的.
平台中的平稳性检验有3种,在此我们选择pp检验,工业增加值指数的一阶差分序列的统计量为-18.7307,小于检验临界值为1%的统计量,因此拒绝原假设,即工业增加值指数的一阶差分序列是平稳序列。使用同样的步骤检验其余的一阶差分序列,得到的结果表明其余的指标的一阶差分序列均为平稳序列,具体结果可见下表。







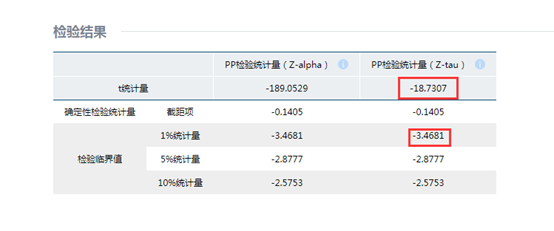
指标 | 统计量 | 1%的临界值 |
IAV | -18.73 | -3.47 |
M2 | -14.61 | -3.47 |
NEER | -7.6996 | -3.47 |
CPI | -13.88 | -3.47 |
API | -13.76 | -3.47 |
PPI | -4.83 | -3.47 |
2.3 VAR建模
序列是一阶单整,因此我们可以对序列建立VAR模型。确定可以建模之后,我们点击计量经济工具箱中的VAR模型,选择6个指标,预测时间和滞后阶数,在此滞后阶数选择2,如果不知道滞后阶数如何选择,可以先默认选择为5,在弹出的结果页中会有最佳的滞后阶数选择结果,可以根据最佳的再次建模。
点击应用,就会弹出结果页,模型的一些结果都在结果页中展示,但是模型的预测结果展示在表格中,方便我们使用这些结果重新分析或者画图。
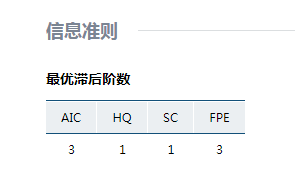
根据AIC准则,我们选择最优的滞后阶数是3, 因此我们重新建模,选择滞后阶数为3,得到的结果在2.4展示。
2.4 结果展示
我们是想要短期预测CPI,因此在结果页中我们只需要看居民消费价格指数作为因变量的模型即可。
由于“货币和准货币期末余额(亿元)-本期数(1阶差分)”,“人民币/100美元(元)-本期数(1阶差分)”,“商品零售价格指数(上年同月=100)-本期数(1阶差分)”的参数估计值未通过检验,表明这3个参数对居民消费价格指数的影响较弱,而且S2的估计值基本为0 ,我们剔除几个解释力度不好的指标,最终选择指标为“工业增加值比上年同期增长(%) (1阶差分)”,“工业生产者出厂价格指数(上年同月=100) (1阶差分)”,“居民消费价格指数(1阶差分)”最终结果如下所示。
其中:S1:工业增加值比上年同期增长(%) (1阶差分)
S2: 工业生产者出厂价格指数(上年同月=100) (1阶差分)
S3:居民消费价格指数(1阶差分)
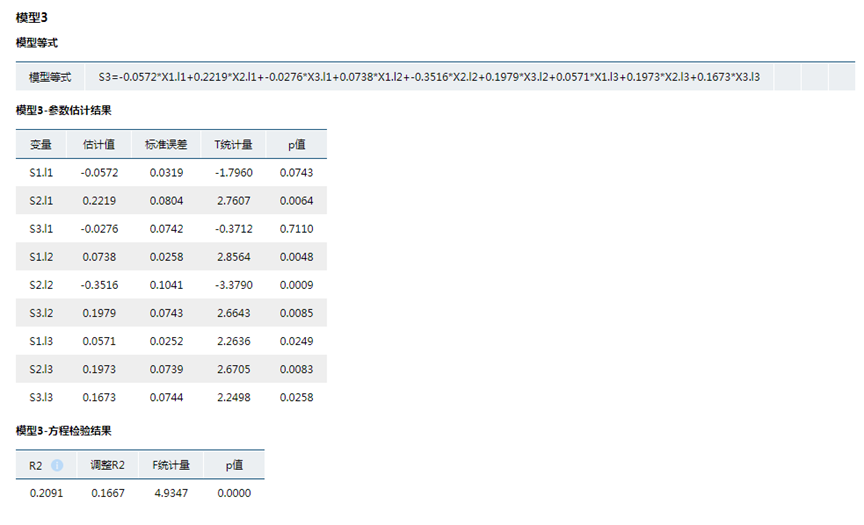
由于工业增加值对居民消费价格指数虽然有一定的影响,但是相对于其他的指标,影响程度可以忽略不计,因此我们只考虑工业生产者价格指数对居民消费价格指数的影响。
滞后一期时,工业生产者出厂价格指数对居民消费价格的影响为正,居民消费价格指数对自身的影响为负,同样的影响也较小,可忽略不计。也就是上个月的PPI上涨会增加工业企业的货物成本,那么则会影响这个月的货物价格或者货物的生产数量,从而使得物价上涨。
滞后二期时,工业生产者出厂价格指数对居民消费价格的影响为负,即这个月的工业生产者出厂价格指数上涨,则会抑制2个月之后的居民消费价格指数的上涨。考虑可能是这个月的PPI上涨会增加工业企业的货物成本,企业为了转嫁上涨造成的成本增加,更为直观的就是下个月增加货物价格,但是由于货物价格的增加,会使得销量下降,企业则会在第二个月促进销量降低货物价格,这个满足一定的市场规律。
滞后三期时,三个指标对居民消费价格指数均为正,并且系数较低,影响较小。也就是表明长期来看,工业值增加指数和工业生产者出厂价格指数的上涨都会对未来的物价上涨起到促进作用,但是由于时间的滞后期较长,因此这个影响较低。
2.5 预测
由于单位根的模都小于1,具体如图所示。
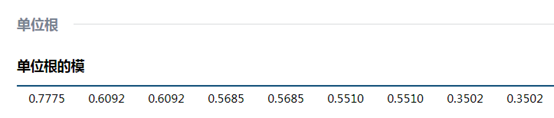
因此估计的模型满足稳定性条件,我们可以对该模型进行预测。预测结果如下所示,由于是一阶差分后的序列,预测结果则需要去除一阶差分,经过计算可以得到居民消费价格指数的预测结果。
时间 | 真实值 | 预测值 | 置信下限 | 置信上限 |
2020年1月 | 105.4 | 104.8306 | 103.8058 | 105.8554 |
2020年2月 | 105.2 | 104.6809 | 103.6314 | 105.7305 |
2020年3月 | 104.3 | 104.6313 | 103.5276 | 105.735 |
2020年4月 | 103.3 | 104.6032 | 103.4706 | 105.7358 |
可以看到VAR模型的预测结果,真实值都在预测的置信区间中,表明预测的结果较好。
三 总结
EPS云分析平台的VAR模型操作简单,经过建模,我们预测未来4个月的居民消费价格指数,从真实值来看,其中1月份最高,后边3个月都略有下降,我们的建模得到的预测值也是同样的变化趋势,并且真实值都在相对应的预测区间之内。以上内容基本上实现了建立向量自回归模型,并给出分析所需的结果。能实现大部分的数据分析的需求。
上一条:云分析之ARIMA模型
下一条:中国城市化与生态环境的耦合度分析