一 全要素生产率

许多实证研究中都有对生产率的测算，生产率是许多实证研究的基础，它通常被解释为总产出中不能由要素投入所解释的“剩余”，该“剩余”就是全要素生产率（TFP）。TFP反应了生产过程中各种投入要素的单位平均产出水平，即投入转化为最终产出的总体效率。

由于估计方法的不同，计算微观企业全要素生产率的方法有很多，最常用的则是OP法，LP法。OP法是假定企业根据当前企业生产率状况，据此作出投资决策，因此用企业的当期投资作为不可观测生产率冲击的代理变量，从而解决了同时性偏差问题。在满足一系列的假定条件下，OP 法可以提供对企业层生产函数的一致估计值。其中一个假定是要求代理变量（投资）与总产出始终保持单调关系，因此投资额为零的样本并不能被估计。而且并非每一个企业每一年都有正的投资，因此在估计过程中企业样本会被丢弃，因此该方法不再使用投资额作为代理变量，而是用中间品投入指标替代，并且从数据的角度出发，工业中间品数据更易获得。即LP方法使得研究者可以根据数据的灵活特点选择代理变量。

二 TFP计算

2.1 数据处理

本次建模的数据来源为EPS中国微观经济数据查询系统中的工业企业数据库，通过简单的统计，在1998-2007年之中，共计有222万条数据，在其中制造业有205万条数据，53万家企业，但是这些数据中有一些指标存在遗漏，缺失等问题，因此在这些数据中，我们选择剔除工业总产值，工业增加值，固定资产为空值和负值的样本，并剔除从业人员数小于8的样本，最终得到192万的数据量，约有企业51万家。我们以该样本作为计算制造业企业全要素生产率的数据样本，计算所需要的指标有：统计年份，企业代码，开业时间，从业人数，固定资产，投资，工业增加值。

在此得到的固定资产，投资和工业增加值都是当年值，因此需要对这些指标做指数平减来消除通货膨胀带来的影响，通过查找一些文献，发现每个人对于这些指标的消胀处理方式由于基期数据选择的不同从而有所差异，本文选择企业所在地区工业品出厂价格指数平减，从而得到固定资产和工业增加值的消除通货膨胀之后的值，其中固定资产的处理还涉及到折旧信息等，对于第一年的固定资产，主要是用该年的固定资产除该年与开业年份之差，之后的固定资产，可以用后一年的减去前一年的固定资产作为当年的固定资产的投资额，而投资则用短期投资和长期投资之和作为最终投资。

2.2数据描述

从该数据可以看到，我国的制造业的企业数量在逐年增加，并且1998年到2001年企业数量增加缓慢，而2001年-2007年的制造业的企业数量增长速度较快，国有企业数量则在下降，表明我国的非国有企业发展速度飞快，1998年国有企业数量占比为28%，工业增加值占比则为36%，而到2007年，我国的国有企业占比减少到2%，表明我国的非国有企业发展相对较快。

2.3 全要素生产率的计算

数据处理之后，我们使用stata采用OP法对该数据样本进行计算，通过计算后得到每个企业的各年份的全要素生产率，然后通过加权可以得到不同分类下的全要素生产率。首先通过计算得到这些企业在这10年的全要素生产率平均增长速度约为4.34%，这个结果是比较接近2004年的年均增长速度。

从下图可以看到，这个生产率的企业数量的分布基本符合正态分布，表明我国制造业的全要素生产率的整体发展水平相对良好。另外可以看到我国的70%的企业的全要素生产率处于4%-6%之间，90%的企业的全要素生产处于3%-7%之间。这个结果表明我国的制造业企业之间的生产率差别较大，因此我们通过对全要素生产率的时间序列，地区分布和行业门类分布进行多方面的多角度的分析。

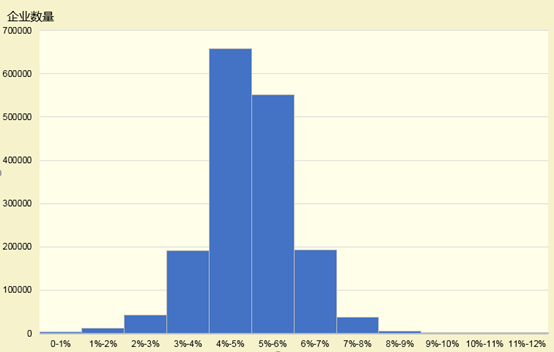
不同范围的TFP的企业数量分布情况

2.3.1 全要素生产率的时序变化

从图中可以看到，全要素生产率1999年开始呈现增长的趋势，虽然工业增加值的增长趋势要比全要素生产率的增长趋势快，但是我国的全部制造业的企业生产效率也在逐年稳定增长，从1999年的3.84%增长到2007年的4.73%。其中2001年的年平均增长率突破4%。表明我国的制造业企业的生产效率在逐年提高，我国的经济发展水平也在逐年提高。

但是1998年的平均TFP值则比较高，从1998年到1999年呈现下降趋势，然后从1999年开始缓慢增长，直到2003年之后才与1998年的TFP水平值持平，猜想可能是由于1998年的国际金融危机导致1999年的我国的制造业企业的生产率水平整体下降。

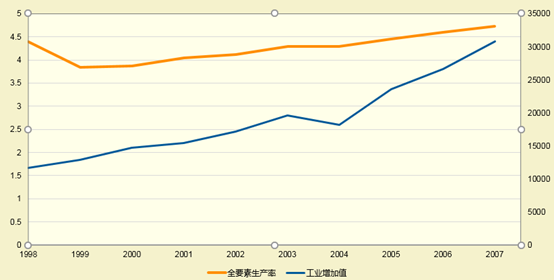
TFP的时间序列图

2.3.2地区分布

全要素生产率在各省的分布如下图所示，各省份相差比较大，颜色为橙色且颜色越深表示值越小，颜色为蓝色且颜色越深表示值越大，从地图中看到西藏的全要素生产率最小，并且全要素生产率较高的省份主要分布在东北沿海地区，中部次之，而西部和东北部较低。这与我国的实际国情也是相符合的。东部地区的上海市，江苏省，福建省和广东省的TFP值都排名前列，而西部地区的贵州省，新疆维吾尔自治区，青海省，甘肃省，和西藏自治区则TFP水平值较低，其中黑龙江省属于东北老工业基地，制造业企业整体依靠资源投入，因此TFP值也不高，但是内蒙古自治区的TFP值在全国31个省份中排名第三，属于除东部地区外TFP最高的省份，然后通过对内蒙古自治区进行分析发现内蒙古的TFP值较高的企业是烟草制品业，有色金属冶炼和压延加工业和石油加工、炼焦及核燃料加工业TFP值排名前三，其中，有色金属冶炼和压延加工业和石油加工制造业的TFP水平值在全国各省份的排名是第二。

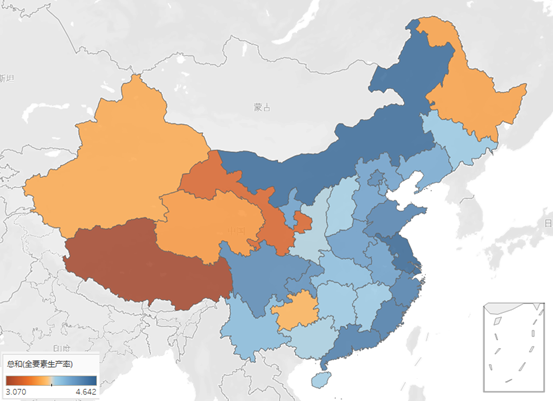
全要素生产率省份分布

从地图来看，我国的制造业企业数量相差不大，只有东部沿海地区的几个省份显示蓝色，表示数量较多，而中部的为浅橙色，表示制造业企业数量较多，西北部以及东北部的企业数量相对较少，这也与企业全要素生产率的大致的地区分布相似，表明我国的企业制造业主要分布在东部沿海地区，并且东部沿海地区的制造业企业TFP也是相对较高的。这也是我国东部地区经济发展较好的主要因素。

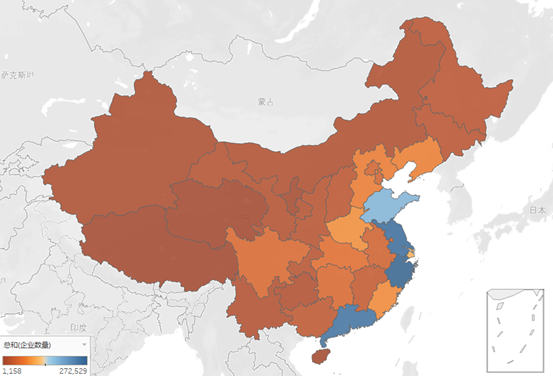
制造业企业数量的全国分布

2.3.3 全要素生产率的行业门类分布

1998年到2007年的29个行业门类中，生产率增长最快的是烟草制品业，石油加工、炼焦及核燃料加工业，有色金属冶炼及压延加工业和通信设备、黑色金属冶炼及压延加工业和电气机械及器材制造业，这些门类的TFP分别为5.55%，4.84%，4.77%，4.66%和4.66%，这些产业多为高新产业，这类产业需要更多高新技术来提高企业生产效率，表明高新技术产业是生产率提高最为快速的产业，而纺织业，印刷业木材加工业和食品制造业等这些产业的生产速率相对较为缓慢，而这些产业的生产过程对技术的要求相对较低，并且具有劳动密集的特点，因此这些传统行业的技术革新是有一定难度的。

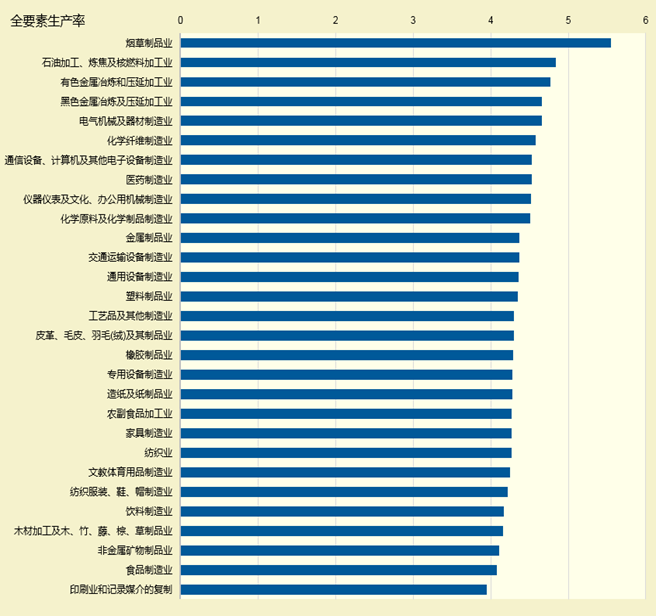
不同行业的TFP对比条形图

2.3.4 不同企业类型的全要素生产率对比

我们统计了不同的企业类型的简单加权的全要素生产率，可以看到，外商参与注册的企业全要素生产率都相对较高，港澳台独资或合资注册的企业的全要素生产率次之，然后是国内大陆的各种私营企业的全要素生产率相对较低，最后是国有企业的全要素生产率最低。因此对于国企的改革是很有必要的。

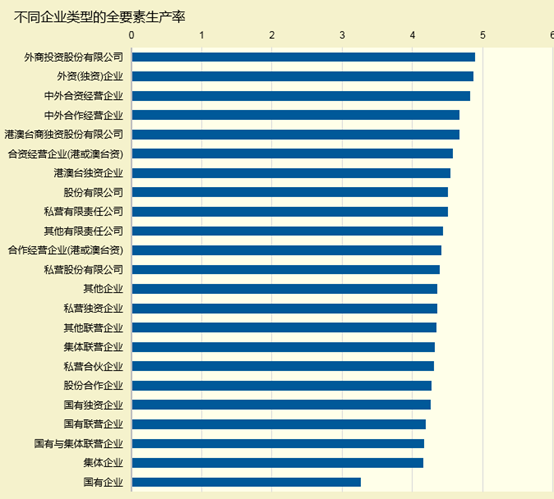
不同注册类型的企业的TFP对比条形图

三 总结

综上，我国制造业的全要素生产率在1998年到2007年的增长速度较为稳定，并且生产率较高的企业主要集中在东部地区，并多为高新产业和外资企业等，这主要是我国的改革开放政策使得东部沿海地区的外商投资企业较多，并且由于我国的工业发展相对较晚，并且私营企业一般为利润导向，的因此形成了东部工业较为发达，私营企业比国营企业效率较高的工业现状。当然这也是我国实施先东部发展，然后东部带动中西部发展较为成功的结果。另外，基于行业的TFP研究表明，属于高新技术产业的企业的全要素生产率表现出较高的水平值和增长值，而传统的劳动密集型产业则TFP水平值相对较低，但是由于这类产业所需廉价劳动力较多，所以对于我国的许多劳动力就业具有很好的稳定作用。

参考文献：

[1] 杨汝岱，2015：《中国制造业企业全要素生产率研究》，《经济研究》02期。

[2] 鲁晓东、连玉君，2012年：《中国工业企业全要素生产率估计:1999-2007》，《经济学季刊》第11卷第2期。