一、引言

彻底消除绝对贫困，一直是人类历史上难以攻克的巨大挑战。根据中国2020年发布的592个国家级贫困县名单绘制省级扶贫重点县的分布数量图(图1)，可以发现，中国作为世界第一人口大国，贫困县的分布十分广阔，占据全国的67.7%，没有扶贫县的省市多分布在东部沿海地区。云南是扶贫县最多的省份，其次是陕西和贵州。

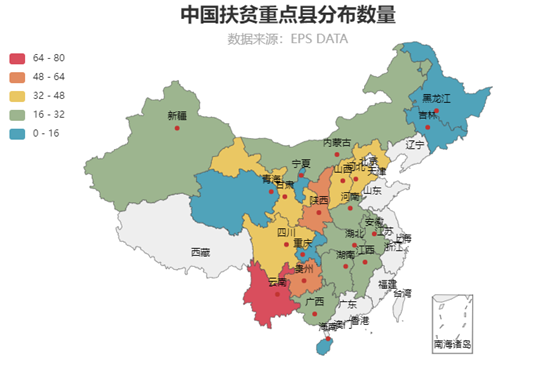
图1 中国2020年扶贫重点县分布数量

除此之外，在2020年底中国贫困县全部摘帽之前，中国的贫困人口排名一直在世界上位居前列。2012年，按照世界银行每人每日1.9美元生活费的标准测算，中国贫困人口为0.88亿，占全世界贫困人口的9.7%。经过多年艰苦的脱贫攻坚，这一比例在2019年底下降到0.64%，贫困人口从2015年的5575万人锐减到551万人，贫困发生率也从5.7%下降到0.6%，毫无疑问，这个成绩是巨大的。本研究用中国扶贫数据库中的数据作为案例进行分析，具有一定的实际意义。

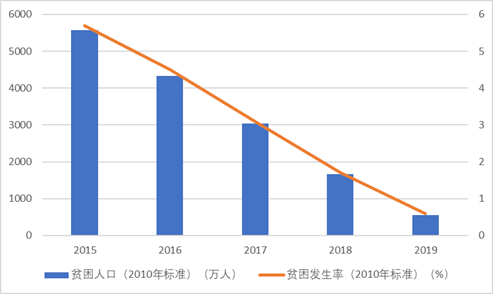
图2 中国2015-2019年贫困数据变化

二、聚类算法介绍

聚类分析作为一种无监督算法，是机器学习中的经典算法之一。其基本思想是“物以类聚，人以群分”，即根据数据的距离或相似度将样本划分为若干组，划分原则是组内样本距离最小化而组间距离最大化。该算法和分类算法的主要区别是分类算法中使用的数据集带有类别标签，而聚类中数据集不需要有类别标签，可以通过聚类将数据聚合成若干个群体。

设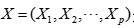是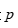维随机向量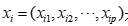，是随机向量X的第i次观测，n次观测组成的矩阵为

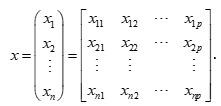
任何两个样本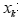和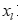之间的相似性或距离，可以通过矩阵x中的第k行和第l行间的相似程度来度量；同样指标之间的相似性可以通过对应列之间的相似性来度量，这两种对样本和指标聚类的方式分别被称为Q型聚类和R型聚类，其中Q型聚类用距离来聚类，R型聚类用相似性聚类。

2.1 距离

测量类内距离的度量方法有：明氏距离、马氏距离和兰氏距离。

（1）明氏距离

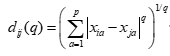
其中。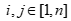

当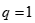时为绝对距离：；

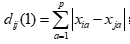当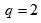时为欧式距离：；

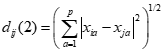当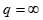时为切比雪夫距离：。

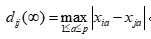（2）马氏距离

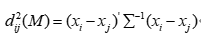
其中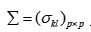为协差阵，，，，。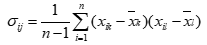

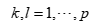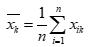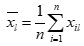样本x到总体G的马氏距离定义为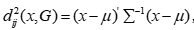,其中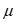为总体的均值向量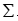，为协方差阵。

马氏距离既排除了各指标之间相关性的干扰，而且还不受各指标量纲的影响。

（3）兰氏距离

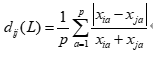
该距离仅适用于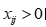的情况，有助于克服指标之间量纲不同带来的影响，但没有考虑指标之间的相关性。该值越小越好。将样本间的距离计算好后，可以得到距离阵D：

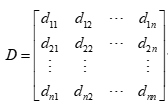
显然，D是一个实对称阵，对角线元素都为0，所以只需要计算上三角部分或下三角部分。根据D可以对n个点进行分类，距离近的点归为一类，距离远的点归为不同的类。

2.2 相似系数

常用的相似系数是指变量之间的相关系数，第i个样本与第j个样本之间的相关系数为：

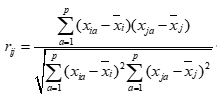
其中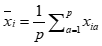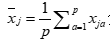，分别是矩阵x第i行和第j行的平均值。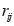的取值范围为[-1, 1]。相关系数阵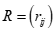，对角线元素。

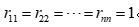2.3 聚类方法

测量类间距离的常用方法有八种，分别是最短距离法、最长距离法、中间距离法、重心法、类平均法、可变类平均法、可变法、离差平方和法。

常用的聚类方法有分层聚类和K-均值聚类两种。

2.3.1 分层聚类(Hierarchical)

分层聚类的核心思想是，把每一个单个的观测都视为一个类，而后计算各类之间的距离，选取最相近的两个类，将它们合并为一个类。新的这些类再继续计算距离，合并到最近的两个类。如此往复，最后就只有一个类。然后用树状图记录这个过程，这个树状图就包含了聚类的信息。

算法：

（1）计算类与类之间的距离，用邻近度矩阵记录；

（2）将最近的两个类合并为一个新的类；

（3）根据新的类，更新邻近度矩阵；

（4）重复（2）（3）；

（5）到只剩下一个类的时候，停止。

2.3.2 K-均值聚类(k-means)

K-均值聚类算法：

（1）选择 K 个初始质心，初始质心随机选择即可，每一个质心为一个类；

（2）把每个观测指派到离它最近的质心，与质心形成新的类；

（3）重新计算每个类的质心，所谓质心就是一个类中的所有观测的平均向量（这里称为向量，是因为每一个观测都包含很多变量，所以我们把一个观测视为一个多维向量，维数由变量数决定）；

（4）重复（2）和（3）.

（5）直到质心不在发生变化时或者达到最大迭代次数时。

2.3.3 分层K-均值算法

由于K均值聚类的结果有时对聚类中心的初始随机选择非常敏感，有人提出分层K-均值算法，是分层聚类和K均值方法的混合。步骤如下：

（1）计算分层聚类；

（2）通过分层聚类结果分成K类；

（3）计算每一类的中心；

（4）用上面得到的中心为K均值聚类的初始值，实行K均值聚类。

在使用K-means算法前，需要给出划分组的数量（K值），但一些数据集并不明确可以分成几组，所以这时要划分组的数量就成了问题，可以借助轮廓系数、聚类结果的稳定性等来判断。

三、聚类算法应用案例

3.1 数据获取与处理

案例使用的数据来自EPS中国扶贫数据库，选取2016年连片特困地区的8个指标，具体包括：贫困人口数量（万人），贫困人口下降幅度（%），贫困发生率水平（%），贫困发生率比上年下降（百分点），人均可支配收入（元），收入名义增速（%），人均消费支出（元），消费支出名义增速（%）。

获得数据后，计算指标相关系数矩阵，得到图3. 然后对数据进行标准化处理用来聚类。

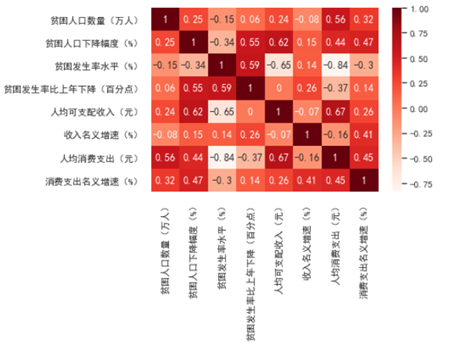
图3 指标相关系数矩阵

3.2 确定K值

根据8种不同类间距离做分层聚类，结果如图4。从图可知，不同的方法所得到的分类结果差异很大，使用ward.D和ward.D2所产生的类比较均匀，可以分成3类，这两种方法都属于离差平方和法。

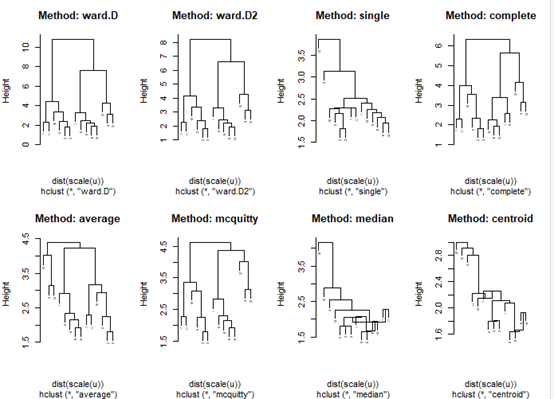
图4 8种不同类间距离聚类结果

再用轮廓系数确定最佳K值，当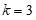时，轮廓系数最大，为0.287，所以最后最终聚为三类。

表1 不同K值下的轮廓系数

3.3 聚类结果

分别用分层聚类、K-均值聚类和分层K-均值聚类对连片特困地区进行聚类。聚类效果如图5-图7，对应的地区编码如表2.分层聚类和分层K-均值聚类的结果相同，K-均值聚类的划分界限虽然有重叠，但是每一类包含的地区都和其他两种聚类方法相同。

表2 连片特困地区编码

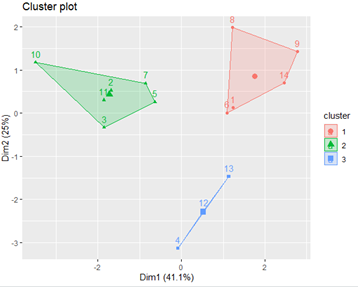
图5 分层聚类

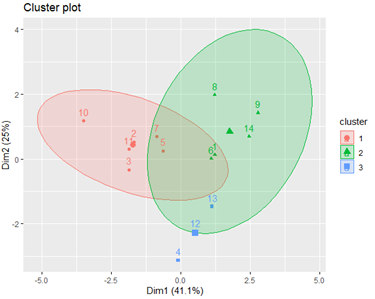
图6 K均值聚类

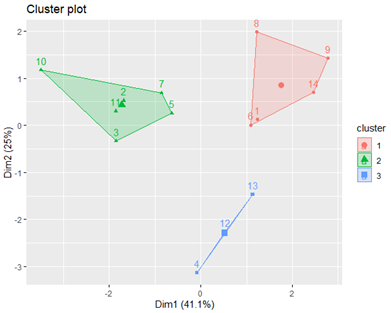
图7 分层K-均值聚类

表3 按照贫困等级聚类的结果

根据连片特困地区在各指标上的数值大小，将聚类结果按贫困等级分别命名为普通贫困、一般贫困、特别贫困，结果如表3.从该结果来看，一般贫困主要分布在我国中西部，普通贫困分布在东北部和东南部，特别贫困分布在北部、最西部。

进一步将连片贫困地区按照“贫困发生率水平-人均消费支出”进行可视化，得到图8.显然贫困发生率水平和人均消费支出呈反比，贫困发生率越高，人均消费支出越低，符合常识。

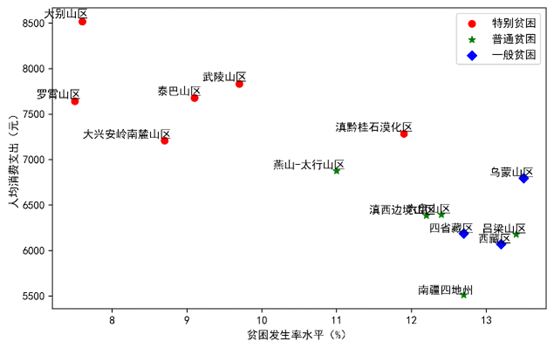
图8 聚类结果可视化

以该聚类分析的结果作为贫困标签，构成训练集，用2014年和2015年连片特困地区相同指标的数据作为测试集，选择决策树作为分类器，所得决策树如图9。对2014年和2015年的数据进行分类，结果如表4.从决策树的结点来看，影响分类的主要指标是：人均消费支出（元）、贫困人口下降幅度（%）、人均可支配收入（元）。

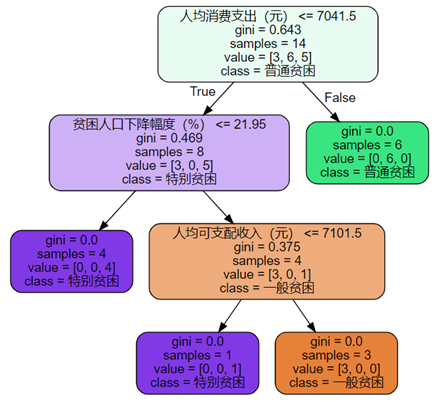
图9 决策树

显然，以2016年的数据作为贫困标准时，2014年14个连片特困地区都属于特别贫困，2015年有3个地区脱离特别贫困，到2016年只剩5个特别贫困地区。这说明中国脱贫攻坚战的效果显著。

表4 2014年-2015年贫困等级