一、 专利申请历年变化

我国统计的三种专利包括实用新型专利，外观专利和发明专利，其中发明专利的技术含量最高。从图1可以看出，自2000年到2017年，我国的国内外三种专利申请数量增长很快，并且在2010年之后的增速比2010年之前的增速要快，但是我国的发明专利申请数量的增长速度明显不如三种专利申请数量的增长速度，自2009年之后，发明专利的增速有所增加，但是增加速度远远低于总的申请数量的增加速度，因此，可以看到发明专利的申请数量与三种专利的申请数量之间的差距逐渐变大。

从图2看到，对比一些发达国家，近年来我国的发明专利申请数量占三种专利申请数量的30%-40%，而发达国家的占比则达到80%及以上。因此，我国的科技还有很大的发展空间。

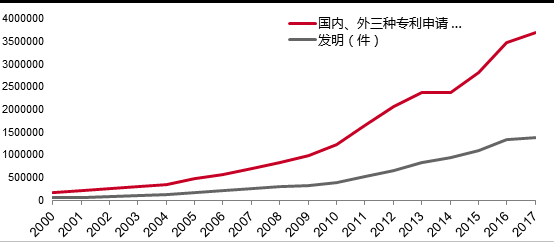
图1：三种专利申请数量的时序变化（数据来源：EPS数据平台）

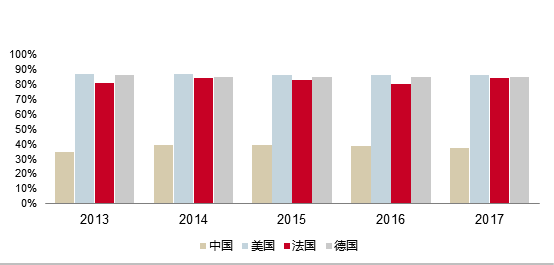
图2：发明专利占申请专利的比值（数据来源：EPS数据平台）

二、专利申请数量地区分布

大致了解了我国的专利申请整体发展水平，需要进一步清楚我国专利申请的地区分布情况。首先用条形图展示2017年全国31个省份的专利申请数量，从图3中看到各省份之间的差距较大，排在前3位的省份分别是广东、江苏与浙江，均属于东部地区。我们想要更多地了解各个省份的空间分布情况，对2008年到2017年的数据进行了分层聚类。

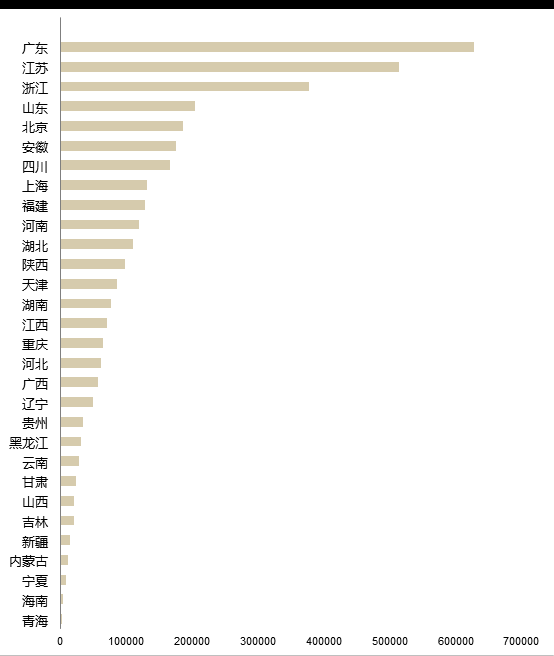
图3：2017年省份的专利申请数条形图（数据来源：EPS数据平台）

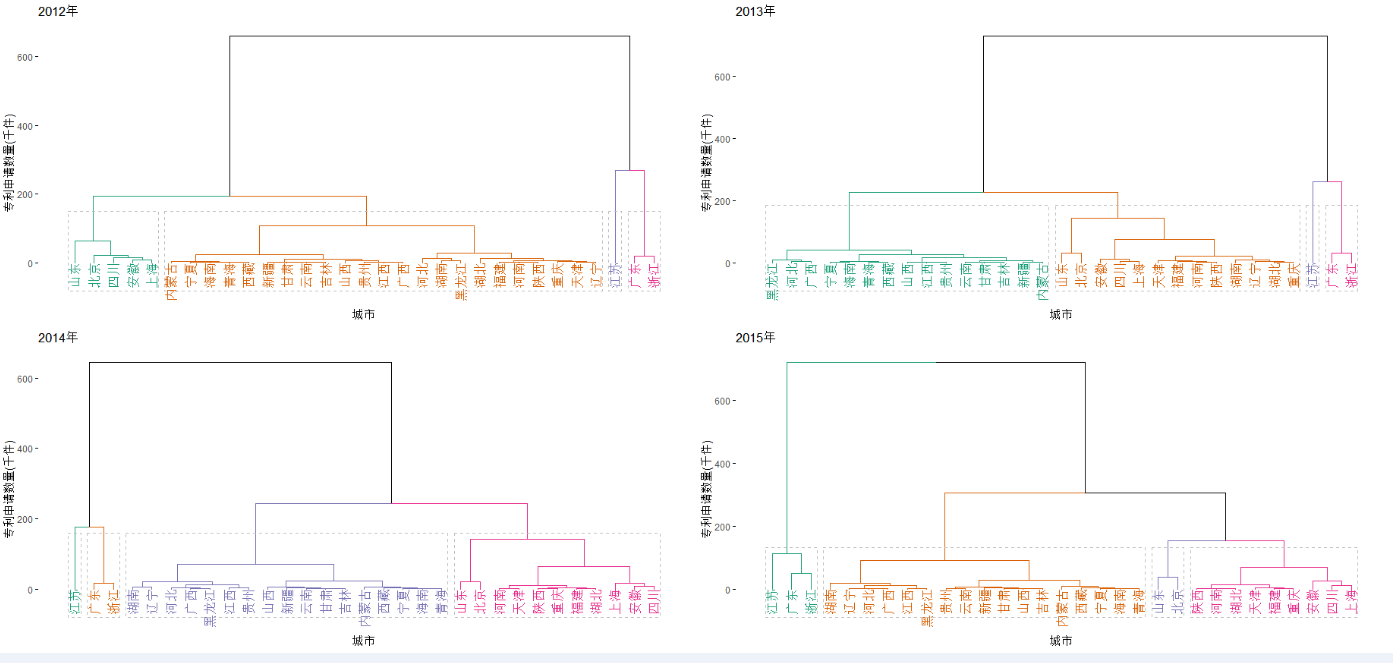
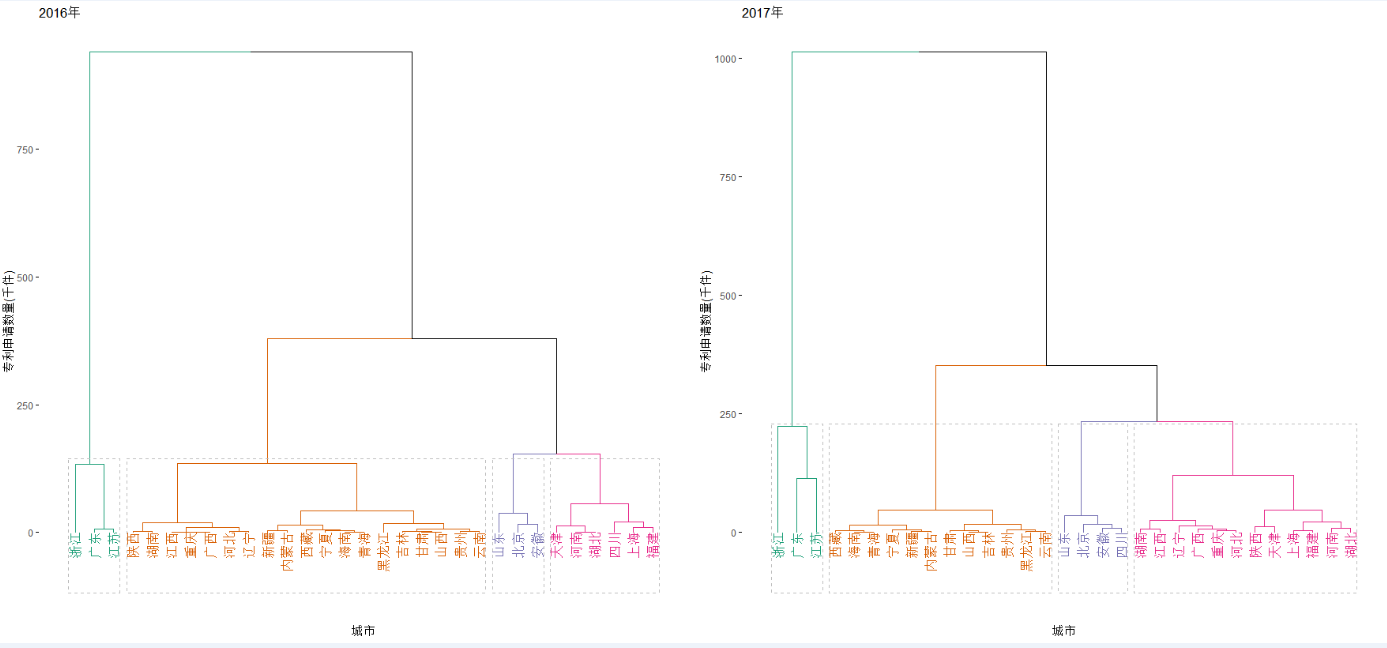
图4：专利申请数的省份聚类分析图（数据来源：EPS数据平台）

表1：专利申请数的聚类结果表

   以上聚类图是把各省份按照专利申请数量通过分层聚类法得到的结果，通过分析可知：

从聚类图和聚类表中可以看出，前两类的科技实力较高，但涉及省份相对较少，并且多数分布在经济比较发达的地区，而且第一类的省份相对稳定，第三类和第四类的科技实力相对较低，这两类分布的省份较多。表明我国的科技实力整体分布不均，地区之间的科技实力差异较大，少数地区科技水平高，多数地区科技水平相对偏低。

三、 专利申请数量的影响因素分析

1． 被解释变量与解释变量的散点图

在研究了专利申请数量的整体发展情况和地区分布情况之后，接下来对专利申请数量用线性回归方式进行建模，分析影响专利申请数量的因素。首先把2006年-2018年的专利申请数量作为被解释变量，选择2005年到2017年的7个指标作为解释变量，分别为“高等学校R&D机构(百个)” ，“R&D人员全时当量（万人年）” ，“R&D经费内部支出(亿元)” ，“R&D项目(课题)数(万项)”，“R&D项目(课题)人员全时当量(万人年)”，“R&D项目(课题)经费内部支出(亿元)”，“发表科技论文(万篇)”。

先画出每个解释变量与被解释变量的散点图，从散点图可以看出这些解释变量与被解释变量之间有线性关系，因此，我们使用最小二乘法进行多元线性回归。

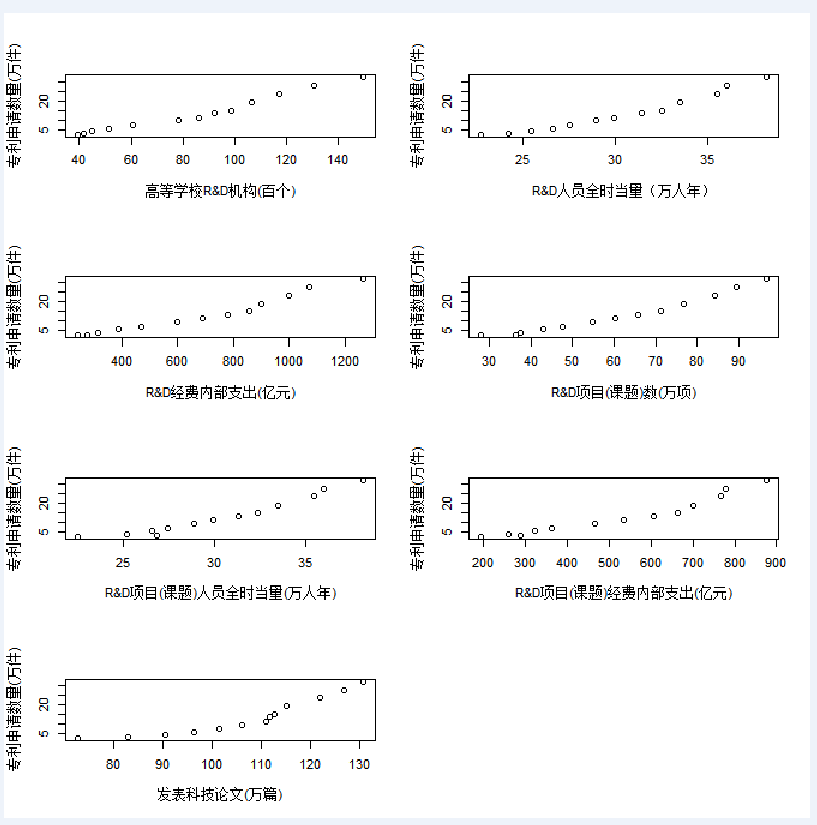
图5：专利申请数与影响因素的散点图（数据来源：EPS数据平台）

2． 建立多元线性回归模型

在建模过程中发现，解释变量“高等学校R&D机构(百个)” ，“R&D人员全时当量（万人年）”等未通过检验，检查发现是变量之间存在很强的多重共线性，因此，使用逐步回归，再次建立回归模型，得到的结果如表2所示，可以看到，模型的系数都通过显著性检验，并且解释变量之间不存在严重多重共线性程度，接下来需要判断模型拟合的优劣。

表2：专利申请数的模型系数表

3． 模型拟合结果判断

线性假设：成分残差图证实了线性假设，说明线性模型对该数据集是比较合适的。

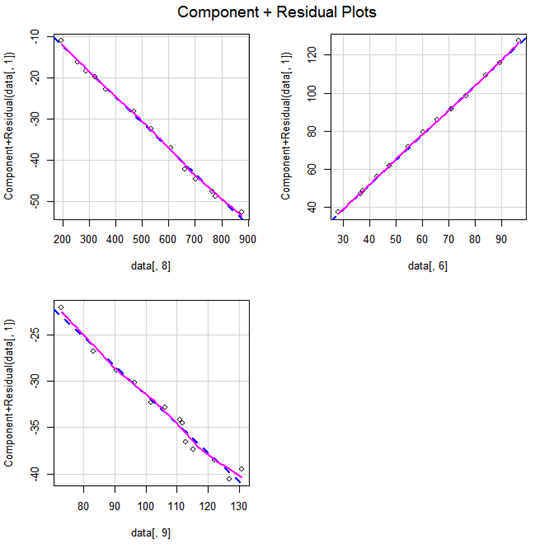
图6：成分残差图

同方差性：p = 0.1158不显著，说明误差方差恒定。从图中可以更方便地看出误差分布的范围，红色线呈现出一条平稳的曲线并没有明显的形状特征，表明方差恒定。

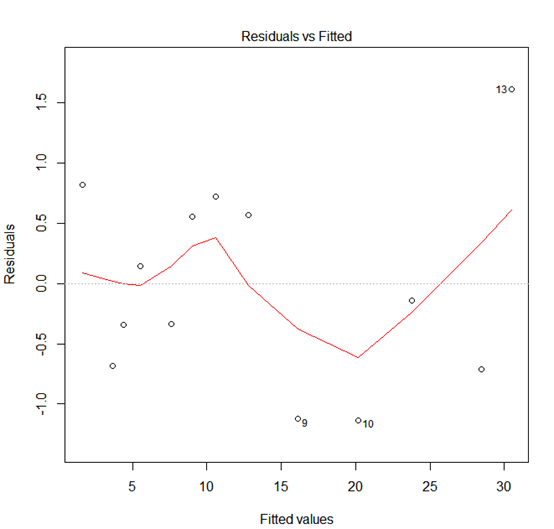
图7：残差分布图

误差自相关检验：由于dw的P值为0.16>0.05，故误差不相关。

残差分析：图8是残差序列图和Quantile-Quantile图，可以看到残差分布比较均匀，表明原本的数据符合线性模型，当Q-Q图上的点贴近y=x这条直线时，表明误差是服从正态分布的。

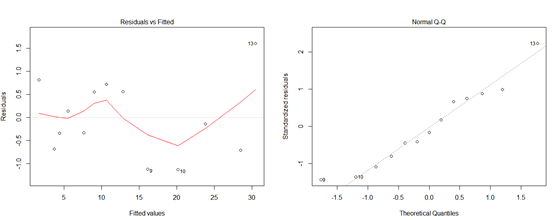
图8：残差图与正态QQ图

4． 最终模型

通过以上的判断，目前拟合的多元线性回归模型结果较好，因此给出最终的模型公式：

专利申请受理数（万件）=1.3009* R&D项目(课题)数(万项)-0.0618* R&D项目（课题）经费内部支出（亿元）-0.3143*发表科技论文（万篇）

模型表明， R&D项目（课题）数每增加1万项，专利申请则增加13009件。R&D项目（课题）经费内部支出每增加1亿元，专利申请则减少618件，发表科技论文数量每增加1万篇，专利申请则减少3143件。

其中R&D项目（课题）经费内部支出的系数较小，对专利的申请数量影响不大。因此产生的抑制作用也可以忽略不计。

发表科技论文会对专利申请数量产生抑制作用，查找其原因，发现建模中使用的数据是高校的专利申请数量以及发表科技论文数量，事实上，我国的许多高校和科研工作者在不断探求科研问题的同时，往往过于注重发表学术论文，而忽略在第一时间申请专利。由于两者对于新颖性和创造性的评价不同，优先发表论文，导致专利申请丧失新颖性，专利审批通过的可能性就基本为零，而高校研究者在科研过程中在专利申请和论文发表两者中会更加注重论文发表。因此，对于同一主题发表学术论文之后，很少会再申请专利，这也会导致发表科技论文对专利申请数产生抑制作用。

5． 模型预测

基于以上的模型，对2018年的专利申请数据进行预测，下表是2018年的自变量的数值，代入模型计算得到的2019年的专利申请数量是35.3146万件。

表3：2018年自变量的值

四、总结

从专利申请数量来看，我国的科技水平在2010年之后发展迅速，但是地区分布不均，科技水平较高的地区相对较少，大部分地区科技水平处于较低的发展现状。建议国家增加第三四类城市的科技投入，缩小地区差异。如果要提高我国整体的科技发展水平，则建议增加R&D项目课题数量，并通过模型预测2019年的专利申请数量是35.3146万件。