一原理介绍

1.1 模型介绍

ARCH模型全称“自回归条件异方差模型”，解决了传统的计量经济学对时间序列变量的第二个假设（方差恒定）所引起的问题。GARCH模型称为广义ARCH模型，是ARCH模型的拓展，由Bollerslev(1986)发展起来的。

GARCH模型主要是用于研究金融资产的波动，基于波动聚集建模，是现代金融时间序列的主要研究模型。在介绍这些模型之前，需要解释一下波动率。传统的时间序列的有一个弱平稳条件，即二阶矩是一个不变的，与时间无关的常数，但是在金融时间序列中，这个条件难以实现，由于金融时间序列的波动性是随时间变化的，，也就是当前的波动率和过去的波动率存在一定的关系。而传统的ARIMA模型则解决不了条件异方差问题，因此需要使用GARCH模型建模，采用GARCH建模后的序列残差即为真正的白噪声，其平方不再具有自相关性。

1.2 模型公式

由于异方差的不同，GARCH模型有许多变形，EPS平台提供了6种模型，分别为ARCH模型，GARCH模型，求和GARCH模型，GARCH均值模型，指数GARCH模型，门限GARCH模型。

?模型结构与分类：

模型包括均值、方差和残差分布三个部分，以Engle(1982)提出的自回归条件异方差模型

ARCH(m) 模型为例：

1.均值方程为：

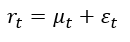
2.方差方程为：

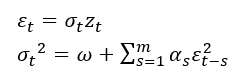
3.其中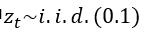，可假定其服从正态分布、学生t分布、广义误差分布（GED）等，也可假定分布有偏。

ARCH模型：

ARCH(1)模型可以解释波动聚集和厚尾现象，但无法解释杠杆效应。ARCH(1)模型如下

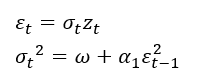
相应的均值和方差为：

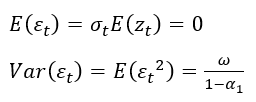
GARCH模型：

标准GARCH：

Bollerslev(1986)提出的标准GARCH(m,n)模型为：

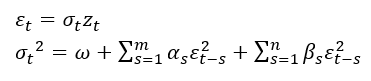
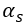和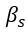分别称为ARCH参数和GARCH参数。

求和GARCH模型（IGARCH）：

以GARCH(1,1)为例，当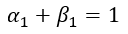时，波动率的方差将趋于无穷大，波动率变成非平稳过程。因此类似于ARIMA模型，IGARCH模型就是单位根GARCH模型，IGARCH(1,1)模型为：

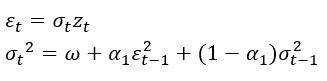
GARCH均值模型（GARCH-M）：

GARCH-M模型考虑波动率对收益率的直接影响，因此在下述模型中  为风险溢价参数：

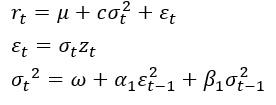
指数GARCH模型（EGARCH）：

?Glosten et al.(1993)，又称为GJR-GARCH模型。当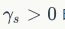时，存在杠杆效应: 

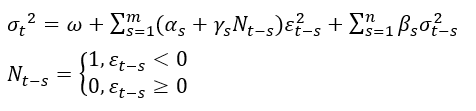
二实证分析

2.1 数据预处理

从EPS的数据库选择2014年1月到2020年12月的上证指数，用该数据来做实证分析。

时序图

首先画出数据的时序图并判断数据的平稳性，从时序图能很明显的看到数据不平稳，因此需要对该数据进行差分处理。

差分

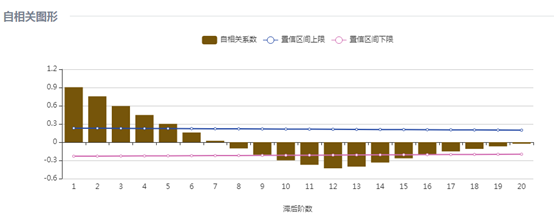
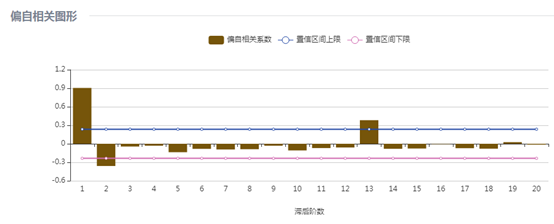
经过一阶差分后根据自相关和偏自相关图发现到12阶时值会超过水平线，因此判断该数据具有季节性，故用12步差分进行处理数据，下图是差分后的图，从图中看到数据没有强烈的波动趋势，因此采用平稳性检验对差分后的数据进行检验。

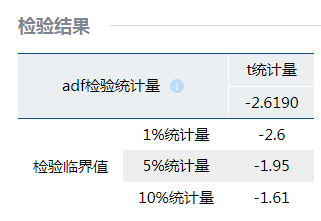
平稳性检验

从结果看出，检验统计量小于1%的统计量，因此拒绝原假设，即数据是平稳序列。可以进行ARMA建模。

2.2 ARIMA建模

根据自相关图和偏自相关图可以给出模型的p,d,q值，在此选择ARIMA（2，0，5）（1，1，1，）作为ARIMA模型参数进行建模，点击ARIMA模型选择适当的参数之后，可以得到ARIMA的模型系数，具体如下图所示，下一步需要对模型残差进行白噪声检验，以判断模型是否合适。

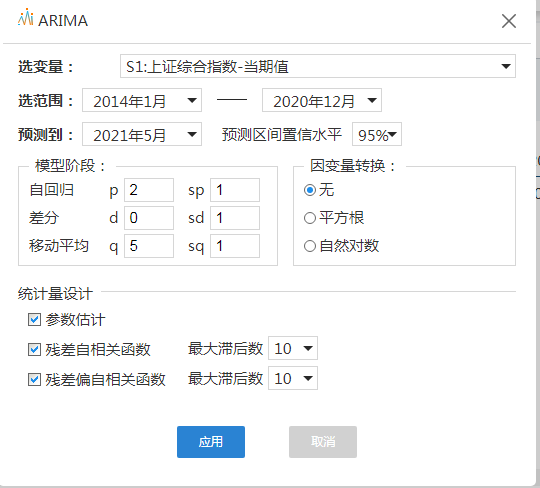
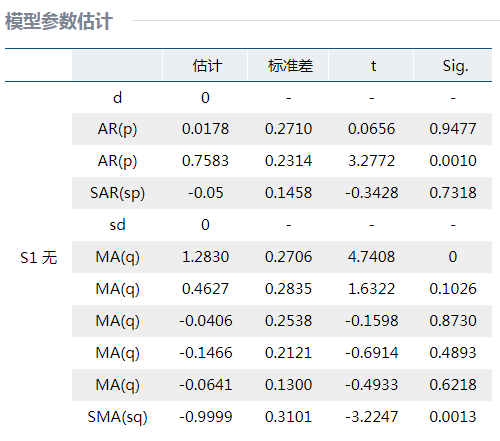
2.3 残差的白噪声检验

根绝结果页显示的白噪声检验结果来看，残差是白噪声。因此该模型目前拟合效果可以。

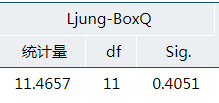
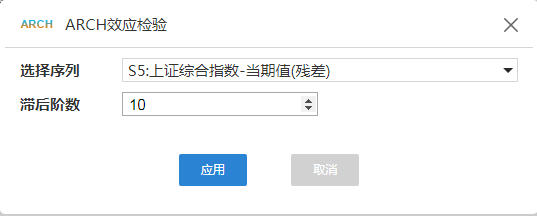
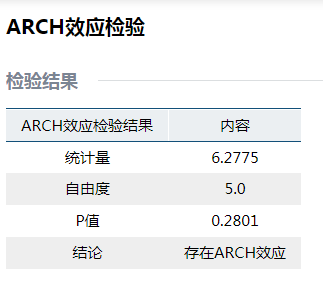
2.5 残差的ARCH效应检验

对残差再进行ARCH效应检验，发现残差存在ARCH效应，因此需要进一步使用GARCH模型进行建模。

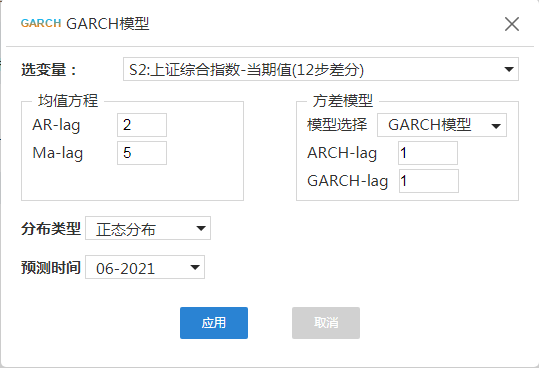
2.6 GARCH建模

在ARMA分别为2和5的条件下，选择GARCH(1,1), GARCH(1,2), GARCH(2,1)，这几个低阶GARCH模型进行建模，选择结果最优的模型作为该数据建模的最终模型，由于GARCH(2,1)模型建模效果不好，并且根据AIC判断，GARCH(1,1)比GARCH(1,2)的AIC数值要小，因此选择GARCH(1,1)作为最优模型。

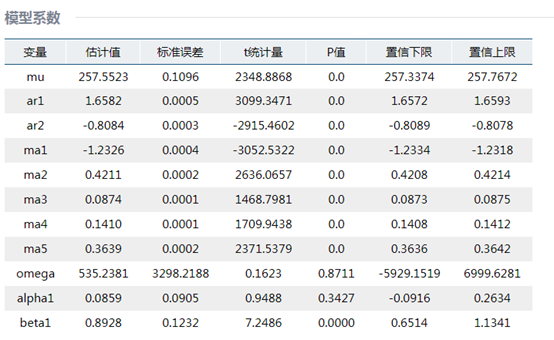
从结果可以看出，

（1）在本次案例中，模型中的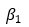系数较大，并通过了显著性检验，表明上证指数波动具有长期记忆性，即过去的价格的波动为长期价格波动具有一定的影响

（2）其中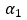大于0，表明指数存在波动聚集

（3）该方程中的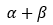接近于1表明条件方差波动具有持续记忆性，说明证券市场对外部冲击的反应以较慢的速度递减，即股市一旦出现较大的波动则在短时间内很难消除该影响。

三 总结

在以上的介绍中，可以知道GARCH模型主要应用于金融计量，而在我们的数据库中时间间隔最少的金融数据则为月度统计数据，因此该模型应用不是很广泛，但是EPS数据平台提供有数据上传功能，想要使用该模型的用户可以上传自己的金融数据进行建模。